
网址:http://www.1010jiajiao.com/paper/timu/5145535.html[举报]
6.“a>1”是“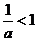 ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
高三单元试题之六:不等式参考答案
一、1.A 2.C 3.C 4.A 5.A 6.A 7.B 8.A 9.A 10.C 11.D 12.B
二、13.[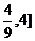 14.
14. 15.{x|0≤x≤4}16.①③
15.{x|0≤x≤4}16.①③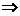 ②④
②④
三、17.解:a>1时,f(x)=logax为增函数,当x∈[2,+∞)时,f(x)有最小值 f(2)=loga2;
0<a<1时f(x)=logax为减函数,当x∈[2,+∞)时,f(x)有最大值 f(2)=loga2;
∵f(x)在x∈[2,+∞)上总有|f(x)|>1成立,
∴a>1时|loga2|>1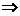 loga2>1
loga2>1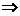 1<a<2;0<a<1时|loga2|>1
1<a<2;0<a<1时|loga2|>1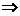 loga2<-1
loga2<-1 <a<1。
<a<1。
∴1<a<2或 。
。
18.由 ,解得
,解得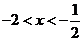 ,∴
,∴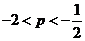 ,∴
,∴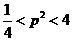 .
.
∴方程z2-2z+5-p2=0的判别式△=4(p2-4)<0,
从而方程z2-2z+5-p2=0无实根.
19.⑴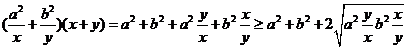
 ,
故
,
故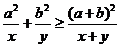 .当且仅当
.当且仅当 ,即
,即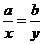 时上式取等号;
⑵由⑴
时上式取等号;
⑵由⑴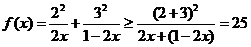 .
当且仅当
.
当且仅当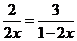 ,即
,即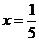 时上式取最小值,即
时上式取最小值,即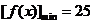 .
.
20.原不等式即(2x-a-1)(x+2a-3)<0,
由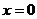 适合不等式故得
适合不等式故得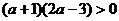 ,所以
,所以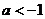 ,或
,或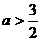 .
.
若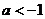 ,则
,则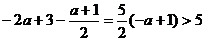 ,∴
,∴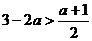 ,
,
此时不等式的解集是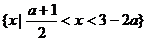 ;
;
若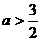 ,由
,由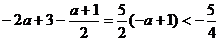 ,∴
,∴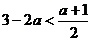 ,
,
此时不等式的解集是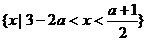 。
。
21.解:(理)∵f(2-x)=f(2+x),∴f(x)的对称轴为x=2,
又∵f(x)的二次项系数大于零,∴f(x)在(-∞,2]上是减函数,在[2,+∞)上是增函数。
⑴当a>0时,2-2ax2≤2,-ax2+2ax-a+2=-a(x-1)2+2≤2,依题意得
2-2ax2>-ax2+2ax-a+2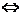 ax2+2ax-a<0
ax2+2ax-a<0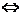 x2+2x-1<0,解得
x2+2x-1<0,解得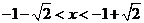
⑵当a<0时,2-2ax2≥2,-ax2+2ax-a+2=-a(x-1)2+2≥2,依题意得
2-2ax2<-ax2+2ax-a+2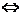 ax2+2ax-a>0
ax2+2ax-a>0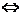 x2+2x-1<0,解得
x2+2x-1<0,解得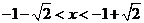
综上所述:原不等式的解集为 。
。
解:(文) ∵f(2-x)=f(2+x),∴f(x)的对称轴为x=2,
又∵f(x)的二次项系数大于零,∴f(x)在(-∞,2]上是减函数,
又∵2- x2≤2,-x2+6x-7=-(x-3)2+2≤2,∴2-
x2≤2,-x2+6x-7=-(x-3)2+2≤2,∴2- x2>-x2+6x-7,
x2>-x2+6x-7,
即x2-12x+18>0,解得 。
。
故原不等式的解集为: 。
。
22.分析:本题为一开放性命题,由于能得到的答案不唯一,使得本题的求解没有固定的模式,学生既能在一般性的推导中找到一个满足条件的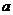 ,也能先猜后证,所找到的实数
,也能先猜后证,所找到的实数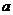 只需满足
只需满足 ,且
,且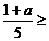 1即可.这种新颖的命题形式有较强的综合性,同时也是对于四个命题考查的一种新尝试,如此命题可以考查学生探究问题、解决问题的能力,符合当今倡导研究性学习的教学方向.
1即可.这种新颖的命题形式有较强的综合性,同时也是对于四个命题考查的一种新尝试,如此命题可以考查学生探究问题、解决问题的能力,符合当今倡导研究性学习的教学方向.
解:已知条件 即
即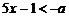 ,或
,或 ,∴
,∴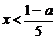 ,或
,或 ,
,
已知条件 即
即 ,∴
,∴ ,或
,或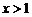 ;
;
令 ,则
,则 即
即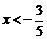 ,或
,或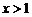 ,此时必有
,此时必有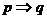 成立,反之不然.
成立,反之不然.
故可以选取的一个实数是 ,A为
,A为 ,B为
,B为 ,对应的命题是若
,对应的命题是若 则
则 ,
,
由以上过程可知这一命题的原命题为真命题,但它的逆命题为假命题.