
网址:http://www.1010jiajiao.com/paper/timu/5145571.html[举报]
20.设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
⑴求证:f(0)=1,且当x<0时,有f(x)>1;
⑵判断f(x)在R上的单调性;
⑶设集合A={(x,y)|f(x2)f(y2)>f(1)},集合B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=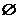 ,求a的取值范围。
,求a的取值范围。
高三单元试题之二:函数参考答案
一、1.B 2.B 3.A 4.B 5.D 6.B 7.C 8.B 9.D 10.B 11.A 12.A
二、13.2 14.f(x),g(x) 15.500 16.(-∞,-1)∪(1,+∞)
三、17.解: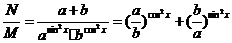 。
。
①
若a>b>0,则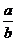 >1,0<
>1,0<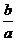 <1。由指数函数的性质知
<1。由指数函数的性质知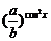 ≥1,0<
≥1,0<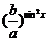 ≤1,∴
≤1,∴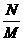 >1,于是N>M;
>1,于是N>M;
②
若a=b>0,则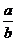 =
=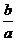 =1,∴
=1,∴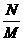 =
=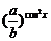 +
+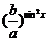 =1+1>1,于是N>M;
=1+1>1,于是N>M;
③ 若0<a<b,同理有N>M。综上所述N>M。
18.解:⑴由题设有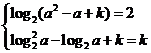 ,∴
,∴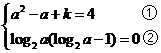
∵a≠1,∴log2a≠0,由②得log2a-1=0,∴a=2,代入①解得k=2。
⑵∵k=2,∴f(x)=x2-x+2=(x- )2+
)2+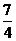 >0。
>0。
∴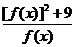 =f(x)+
=f(x)+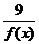 ≥
≥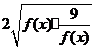 =6。当且仅当f(x)=
=6。当且仅当f(x)=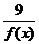 ,即[f(x)]2=9时取等号。∵f(x)>0,∴f(x)=3时取等号。即x2-x+2=3,解得x=
,即[f(x)]2=9时取等号。∵f(x)>0,∴f(x)=3时取等号。即x2-x+2=3,解得x=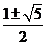 。当x=
。当x=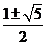 时,
时,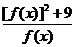 取最小值。
取最小值。
19.解:⑴由题意,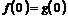 ,
,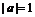 又
又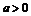 ,所以
,所以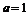 。
。
⑵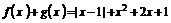
当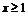 时,
时,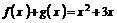 ,它在
,它在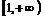 上单调递增;
上单调递增;
当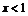 时,
时,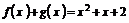 ,它在
,它在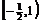 上单调递增。
上单调递增。
20.解:⑴f(m+n)=f(m)f(n),令m=1,n=0,则f(1)=f(1)f(0),且由x>0时,0<f(x)<1,∴f(0)=1;设m=x<0,n=-x>0,∴f(0)=f(x)f(-x),∴f(x)=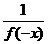 >1。
>1。
⑵设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1,∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,∴f(x)在R上单调递减。
⑶∵f(x2)f(y2)>f(1),∴f(x2+y2)>f(1),由f(x)单调性知x2+y2<1,又f(ax-y+2)=1=f(0),
∴ax-y+2=0,又A∩B=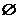 ,∴
,∴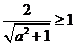 ,∴a2+1≤4,从而
,∴a2+1≤4,从而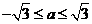 。
。
21.解:⑴依题意,设B(t, 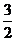 t),A(-t,
t),A(-t, 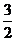 t)(t>0),C(x0,y0)。∵M是BC的中点,∴
t)(t>0),C(x0,y0)。∵M是BC的中点,∴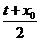 =1,
=1,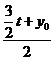 =m,∴x0=2-t,y0=2m-
=m,∴x0=2-t,y0=2m-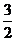 t。在△ABC中,|AB|=2t,AB边上的高h=y0-
t。在△ABC中,|AB|=2t,AB边上的高h=y0-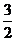 t=2m-3t。∴S=
t=2m-3t。∴S= |AB|.h=
|AB|.h= .2t.(2m-3t)=-3t2+2mt,t∈(0,1]。
.2t.(2m-3t)=-3t2+2mt,t∈(0,1]。
⑵S=-3t2+2mt=-3(t-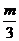 )2+
)2+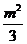 ,t∈(0,1]。若
,t∈(0,1]。若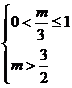 ,即
,即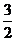 <m≤3。当t=
<m≤3。当t=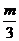 时,Smax=
时,Smax=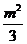 ,相应的C点坐标是(2-
,相应的C点坐标是(2-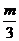 ,
,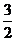 m)。若
m)。若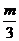 >1,即m>3时,S=f(t)在区间(0,1]上是增函数,∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-
>1,即m>3时,S=f(t)在区间(0,1]上是增函数,∴Smax=f(1)=2m-3,相应的C点坐标是(1,2m-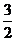 )。
)。
22.⑴证明:由题设条件可知,当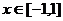 时,有
时,有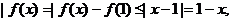
即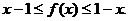
⑵证法一:对任意的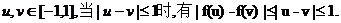
当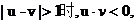 不妨设
不妨设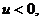 则
则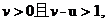
所以,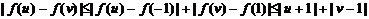
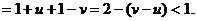 综上可知,对任意的
综上可知,对任意的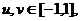 都有
都有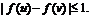
证法二:由⑴可得,当
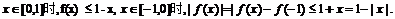
所以,当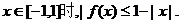 因此,对任意的
因此,对任意的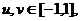
当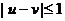 时,
时,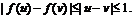 当
当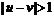 时,有
时,有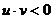
且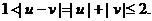
所以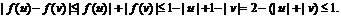
综上可知,对任意的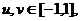 都有
都有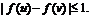
⑶答:满足所述条件的函数不存在.
理由如下,假设存在函数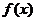 满足条件,则由
满足条件,则由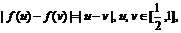
得 又
又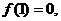 所以
所以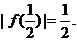 ①
①
又因为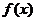 为奇数,所以
为奇数,所以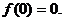 由条件
由条件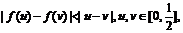
得 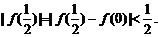 ② ①与②矛盾,所以假设不成立,即这样的函数不存在.
② ①与②矛盾,所以假设不成立,即这样的函数不存在.