
网址:http://www.1010jiajiao.com/paper/timu/5145635.html[举报]
11. ; 12。 ;
数 学(理)
参考答案
一、选择题:(本题每小题5分,共50分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
A |
C |
D |
B |
B |
C |
D |
A |
C |
D |
二、填空题:(本题每小题4分,共16分)
11. 30 12.2
13.4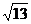 14.25
14.25
三、解答题(本大题6小题,共84分 解答应写出文字说明,证明过程或演算步骤)
解答应写出文字说明,证明过程或演算步骤)
15、解答: (1)∵|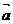 |=1,∴(sinx-1)2+(cosx-1)2=1,
|=1,∴(sinx-1)2+(cosx-1)2=1,
即sinx+cosx=1,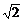 sin(x+
sin(x+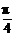 )=1,
…………4分
)=1,
…………4分
sin(x+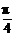 )=
)=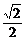 ,又
,又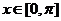 ∴x=0或
∴x=0或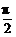 ………………7分
………………7分
(2)∵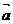 .
. =sin(x+
=sin(x+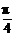 )-
)-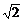 .
.
∴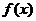 =sin(x+
=sin(x+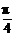 )-
)-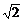 ,
………………10分
,
………………10分
由题意得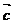 =(-
=(-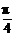 ,-
,-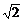 ).
………………14分
).
………………14分
16、解:(1)根据题意ξ的取值应是4,5,6,7
“ξ=4”表示甲胜4场或乙胜4场
∴P(ξ=4)=2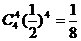 ;(2分)
;(2分)
“ξ=5”表示甲胜第5场且前4场中胜3场,或乙胜第5场且前4场中胜3场
∴P(ξ=5)=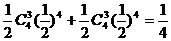 ;(4分)
;(4分)
“ξ=6”表示甲胜第6场且前5场中胜3场,或乙胜第6场且前5场中胜3场
∴P(ξ=6)=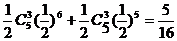 ;(6分)
;(6分)
“ξ=7”表示甲胜第7场且前6场中胜3场,或乙胜第7场且前6场中胜3场
∴P(ξ=7)=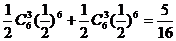 ; (8分)
; (8分)
因此随机变量ξ的分布列为
|
ξ |
4 |
5 |
6 |
7 |
|
P |
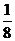 |
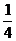 |
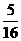 |
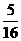 |
并且Eξ=4×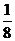 +5×
+5×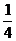 +6×
+6×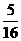 +7×
+7×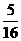 =
=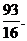 (10分)
(10分)
(2)用随机变量η表示举行一次这样比赛的所需费用,则根据条件,知η=32ξ+200,
由于Eξ=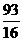 ,所以Eη=E(32ξ+200)=32Eξ+200=386.
,所以Eη=E(32ξ+200)=32Eξ+200=386.
因此举行一次这样的比赛所需费用平均为386元. (14分)
17、(Ⅰ)证明:正方形ABCD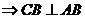 ∵面ABCD⊥面ABEF且交于AB,
∵面ABCD⊥面ABEF且交于AB,
∴CB⊥面ABEF
∵AG,GB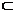 面ABEF, ∴CB⊥AG,CB⊥BG
面ABEF, ∴CB⊥AG,CB⊥BG
又AD=2a,AF= a,ABEF是矩形,G是EF的中点,
∴AG=BG=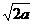 ,AB=2a, AB2=AG2+BG2,∴AG⊥BG ∵CG∩BG=B ∴AG⊥平面CBG 而AG
,AB=2a, AB2=AG2+BG2,∴AG⊥BG ∵CG∩BG=B ∴AG⊥平面CBG 而AG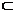 面AGC, 故平面AGC⊥平面BGC …………5分
面AGC, 故平面AGC⊥平面BGC …………5分
(Ⅱ)解:如图,由(Ⅰ)知面AGC⊥面BGC,且交于GC,在平面BGC内作BH⊥GC,垂足为H,则BH⊥平面AGC, ∴∠BGH是GB与平面AGC所成的角
∴在Rt△CBG中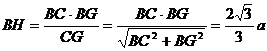 又BG=
又BG=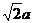 ,
,
∴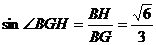 ……………………9分
……………………9分
(Ⅲ)由(Ⅱ)知,BH⊥面AGC 作BO⊥AC,垂足为O,连结HO,则HO⊥AC,
∴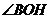 为二面角B-AC-G的平面角 在
为二面角B-AC-G的平面角 在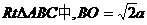
在Rt△BOH中, 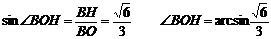
即二面角B-AC-G的大小为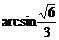 ………………14分
………………14分
18、 (1)解:将点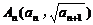 代入
代入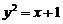 中得
中得
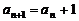 即
即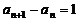 ∴
∴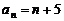 3分
过点(0,1)且方向向量为(1,2)的直线为
3分
过点(0,1)且方向向量为(1,2)的直线为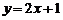 ∴
∴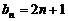 6分
(2) 对任意正整数n,不等式
6分
(2) 对任意正整数n,不等式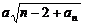 ≤
≤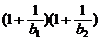 …
…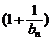 成立
即a≤
成立
即a≤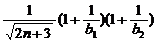 …
…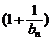 对任意正整数n成立 8分
记
对任意正整数n成立 8分
记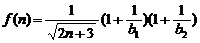 …
…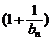 则
则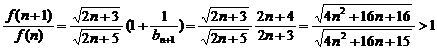 12分
∴
12分
∴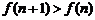 ,即f (n)递增
故
,即f (n)递增
故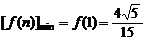 ,∴0<a≤
,∴0<a≤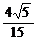
 14分
14分
19、 解:(Ⅰ)以BC所在直线为x轴,线段BC的中点O为原点,线段BC的中垂线为y轴建立坐标系如图
设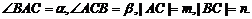 …………2分
…………2分
|
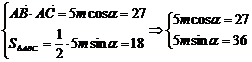
两式平方相加,得m=9 ………………4分
………………4分
又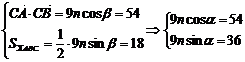
两式平方相加,得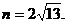 ………………6分
………………6分
设双曲线的方程为 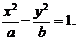 由双曲线的定义,
由双曲线的定义,
有2a=||AC|-|AB||=|m-5|=4,即a=2 又2c=
又2c=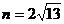 ,即
,即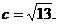
∴b2=c2-a2=9 ∴双曲线E的方程为
∴双曲线E的方程为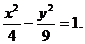 ……8分
……8分
(Ⅱ)假设存在满足条件的直线l,使l与双曲线E交于不同两点M、N,
并设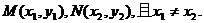 由
由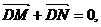 知点D是线段MN的中点,
知点D是线段MN的中点,
∴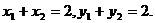 …………10分
…………10分
由于点M、N都在双曲线E上,
∴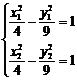
 将两式相减,得
将两式相减,得
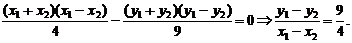
此时直线l的方程为 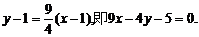 ……12分
……12分
但由
∴不存在满足条件的直线l ………………14分
………………14分
20、解:(1)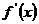 =
=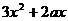 …………2分
…………2分
依题意得k=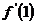 =3+2a=-3, ∴a=-3
=3+2a=-3, ∴a=-3
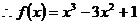 ,把B(1,b)代入得b=
,把B(1,b)代入得b=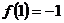
∴a=-3,b=-1 …………4分
(2)令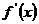 =3x2-6x=0得x=0或x=2
=3x2-6x=0得x=0或x=2
∵f(0)=1,f(2)=23-3×22+1=-3
f(-1)=-3,f(4)=17
∴x∈[-1,4],-3≤f(x)≤17
要使f(x)≤A-1989对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1989
∴A≥2006。 …………8分
(1)
已知g(x)=-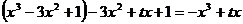
∴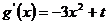
∵0<x≤1,∴-3≤-3x2<0,
①
当t>3时,t-3x2>0,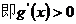
∴g(x)在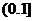 上为增函数,
上为增函数,
g(x)的最大值g(1)=t-1=1,得t=2(不合题意,舍去)…………10分
②
当0≤t≤3时, 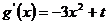
令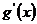 =0,得x=
=0,得x=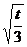
列表如下:
|
x |
(0, 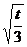 ) ) |
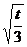 |
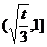 |
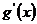 |
+ |
0 |
- |
|
g(x) |
↗ |
极大值 |
↘ |
g(x)在x=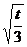 处取最大值-
处取最大值-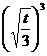 +t
+t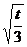 =1
=1
∴t=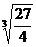 =
=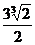 <
<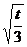 3
3
∴x=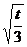 <1
<1
③当t<0时,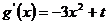 <0,∴g(x)在
<0,∴g(x)在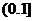 上为减函数,
上为减函数,
∴g(x)在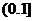 上为增函数,
上为增函数,
∴存在一个a=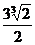 ,使g(x)在
,使g(x)在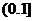 上有最大值1。…………14分
上有最大值1。…………14分