网址:http://www.1010jiajiao.com/paper/timu/5145933.html[举报]
20.已知数列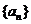 满足:
满足: ,且
,且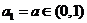 .
.
(1)用数学归纳法证明: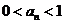 ;(2)试求
;(2)试求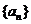 的通项公式;(3)对于
的通项公式;(3)对于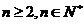 ,求证:
,求证: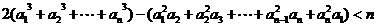 .
.
提示:(2)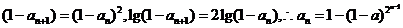
(3)分析:由已知可得: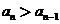
方法1: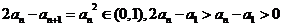 ,所以左边=
,所以左边=
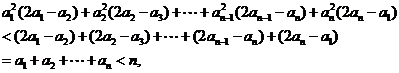
方法2: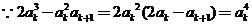
故:左边=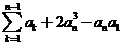
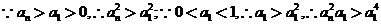
故:左边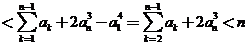
方法3:由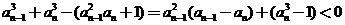
又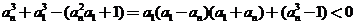
累加可证
方法4:对上面方法3的一种推广:
对任意的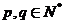 ,
,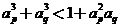
证明如下:若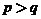 ,
,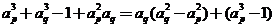
 ,
,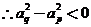 ,故得证
,故得证
若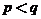 ,则
,则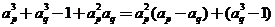
同理可证
这样,利用上述命题,对左边各式进行任意组合,便可证明
(文科)设等比数列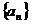 的公比为
的公比为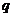 ,前n项和
,前n项和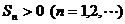 .(1)求
.(1)求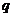 的取值范围;(2)设
的取值范围;(2)设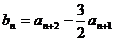 ,记
,记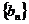 的前n项和为
的前n项和为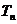 ,试比较
,试比较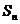 与
与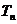 的大小.
的大小.
解:(2005全国卷Ⅰ)
(1)因为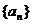 是等比数列,
是等比数列,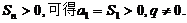 当
当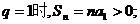
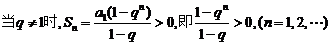
上式等价于不等式组: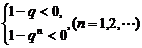 ①
①
或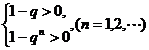 ②
②
解①式得q>1;解②,由于n可为奇数、可为偶数,得-1<q<1.
综上,q的取值范围是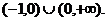
(2)由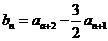 得
得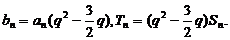
于是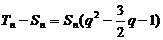
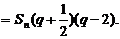
又∵ >0且-1<
>0且-1<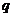 <0或
<0或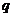 >0
>0
当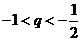 或
或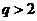 时
时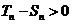 即
即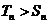
当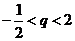 且
且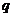 ≠0时,
≠0时,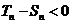 即
即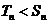
当 或
或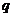 =2时,
=2时,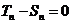 即
即