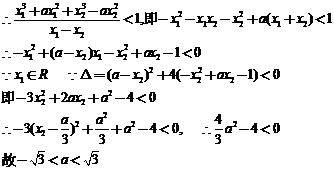网址:http://www.1010jiajiao.com/paper/timu/5145948.html[举报]
11.已知函数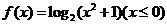 ,则
,则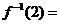 .
.
参考答案:
一、选择题
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
A |
C |
D |
A |
A |
C |
B |
B |
B |
C |
二.填空题:
11.
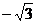 12.
12. 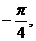
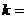 1
.
1
.
13. 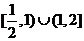 . 14. {2,4,3}(或{1,2,
. 14. {2,4,3}(或{1,2,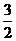 }等
}等
三、解答题:
15. 解:解法一 由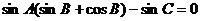
得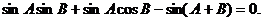
所以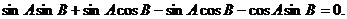
即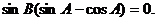
因为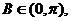 所以
所以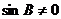 ,从而
,从而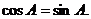
由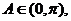 知
知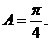 从而
从而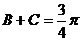 .
.
由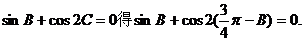
即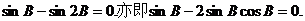
由此得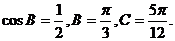 所以
所以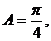
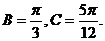
解法二:由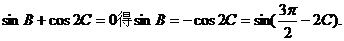
由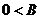 、
、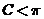 ,所以
,所以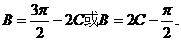
即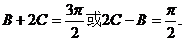
由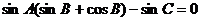 得
得 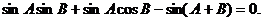
所以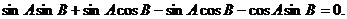
即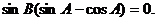 因为
因为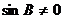 ,所以
,所以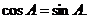
由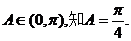 从而
从而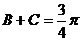 ,知B+2C=
,知B+2C=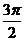 不合要求.
不合要求.
再由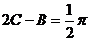 ,得
,得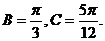 所以
所以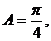
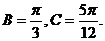
16.解(Ⅰ)如果第一次出现红灯,则接着又出现红灯的概率是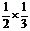 ;如果第一次出现绿灯,则接着出现红灯的概率为
;如果第一次出现绿灯,则接着出现红灯的概率为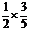 .
.
综上,第二次出现红灯的概率为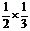 +
+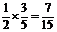 .
.
(Ⅱ)由题意,三次发光中,出现一次红灯、两次绿灯的情况共有如下三种方式:
①当出现绿、绿、红时的概率为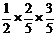 ;②当出现绿、红、绿时的概率为
;②当出现绿、红、绿时的概率为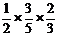 ;
;
③当出现红、绿、绿时的概率为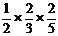 ;
;
所以三次发光中,出现一次红灯、两次绿灯的概率为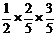 +
+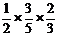 +
+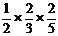 =
=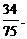
17. 解:(Ⅰ)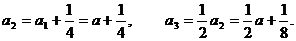
(Ⅱ)因为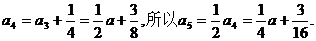
所以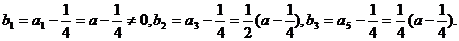
猜想: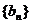 是公比为
是公比为 的等比数列.
的等比数列.
证明如下:
因为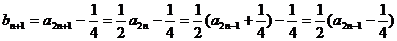
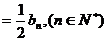
所以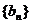 是首项为
是首项为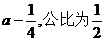 的等比数列.
的等比数列.
(Ⅲ)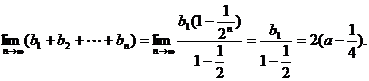
18.解:(1)不能,取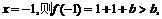
即存在点(-1,2+b)在函数图象上,且在直线 的上方;
的上方;
(2)由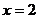 是方程
是方程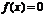 的一个根,得
的一个根,得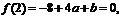 即
即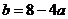
又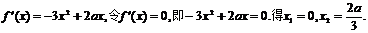
又函数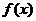 在[0,2]上是增函数,
在[0,2]上是增函数,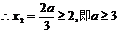 ,
,
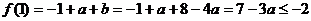
(3)设任意不同的两点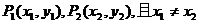 ,则
,则