
网址:http://www.1010jiajiao.com/paper/timu/5145981.html[举报]
18.(本题满分12分) 已知数列
已知数列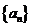 的前
的前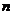 项的和
项的和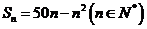

①求证: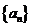 是等差数列;
是等差数列;
②设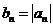 ,求数列
,求数列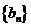 的前
的前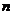 项的和
项的和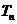

参考答案及评分标准(理科)
一、选择题
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
B |
B |
D |
C |
A |
C |
B |
D |
B |
C |
A |
D |
二、填空题
13.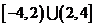 ;14
;14 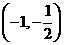 ;15
;15 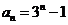 ;16 ①②③④
;16 ①②③④ 
三、解答题
17.(12分)解:因为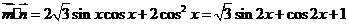 2分
2分
所以 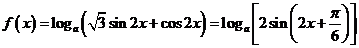 4分
4分
故 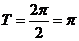 5分
5分
令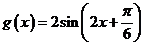 ,则
,则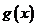 的单调递增的正值区间是
的单调递增的正值区间是
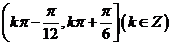 ,
,
单调递减的正值区间是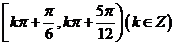 9分
9分
当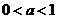 时,函数
时,函数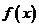 的单调递增区间为
的单调递增区间为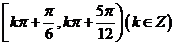
当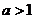 时,函数
时,函数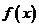 的单调递增区间为
的单调递增区间为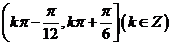
(注:区间为开的不扣分)12分
18.(12分)解:① 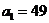 ,当
,当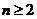 时,
时,
有 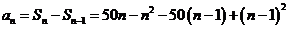
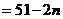
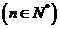 3分
3分
所以 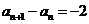 ,故
,故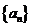 是首项为49,公差为
是首项为49,公差为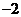 的等差数列 5分
的等差数列 5分
②若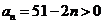 ,则
,则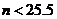 6分
6分
设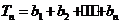 ,当
,当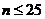 时,则
时,则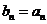 ,此时,
,此时,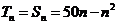 ; 8分
; 8分
当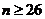 时,
时,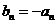 ,而
,而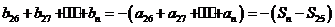
所以 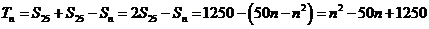 11分
11分
综合所得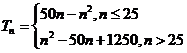 12分
12分
19.(12分)①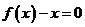
令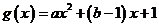
因为 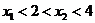 ,
,
所以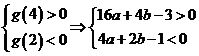
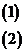 3分
3分
(解法1)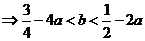
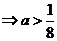
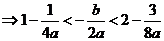
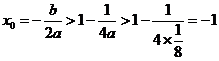 6分
6分
(解法2)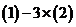 得
得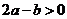
所以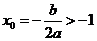
②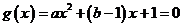
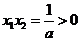 ,即
,即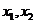 同号
同号
因为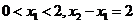
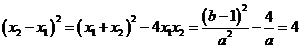
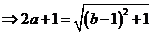 9分
9分
又因为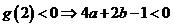
所以
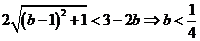 12分
12分
20.(12分)解:因为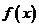 在R上为奇函数,又在
在R上为奇函数,又在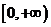 上是增函数
上是增函数
所以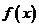 在R上也是增函数,且
在R上也是增函数,且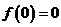 4分
4分
因为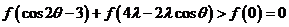
所以 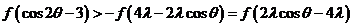
故 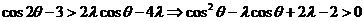
要使不等式对任意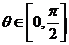 恒成立,只要
恒成立,只要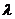 大于函数
大于函数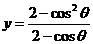 的最大值即可
的最大值即可 8分
8分
令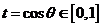 ,则求函数
,则求函数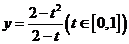 的最大值,
的最大值,
方法1(求导)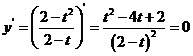
解得: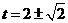 ,因
,因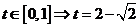
当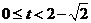 ,时,
,时,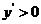 ;当
;当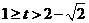 时,
时,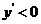
故 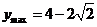 ,因此
,因此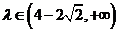 12分
12分
方法2(判别式)把函数变形为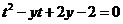
设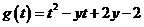 ,即
,即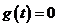 在
在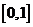 上有解
上有解
当 时,必须
时,必须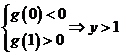 且
且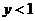 ,矛盾;
,矛盾;
当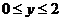 时,
时,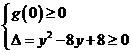 或
或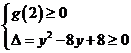
或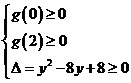
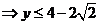 或
或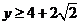
此时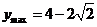 ;
;
当 时,必须
时,必须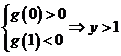 且
且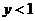 ,矛盾;
,矛盾;
方法3(不等式)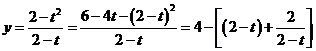
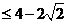 ,此时
,此时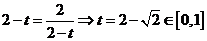
21.(16分)①依题意有 第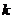 次播放了:
次播放了: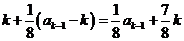 3分
3分
因此 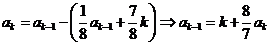 6分
6分
②因为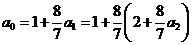 8分
8分
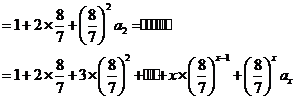
因为 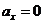 ,所以
,所以 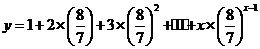 10分
10分
用错位相减法求和得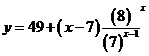 14分
14分
因为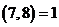 ,故
,故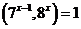 ,而
,而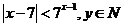 ,
,
则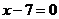 ,即
,即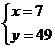 16分
16分
22.(16分)①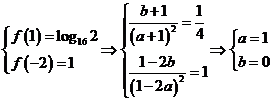
所以 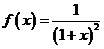 4分
4分
②(用数学归纳法做的酌情给分)
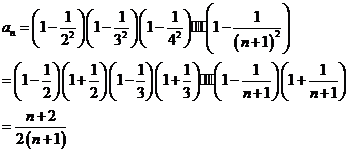
8分
③(用其它方法做的酌情给分)
不等式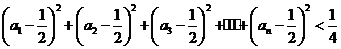 等价于
等价于
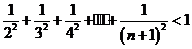 10分
10分
因为
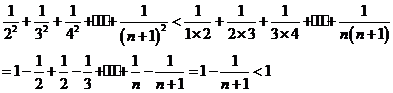
14分