
网址:http://www.1010jiajiao.com/paper/timu/5146164.html[举报]
基本知识点:
(1)求解直线与圆锥曲线的位置关系的基本方法是解方程组,进而转化为一元二次方程后利用判别式,应特别注意数形结合的办法。
(2)注意韦达定理的应用。
弦长公式:斜率为k的直线被圆锥曲线截得弦AB,若A、B两点的坐标分别是A(x1,y1),B(x2,y2)则
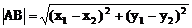
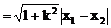

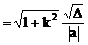
(3)注意斜率不存在的情况的讨论和焦半径公式的使用。
(4)有关中点弦问题
<1>已知直线与圆锥曲线方程,求弦的中点及与中点有关的问题,常用韦达定理。
<2>有关弦的中点轨迹,中点弦所在直线方程,中点坐标问题,有时采用“差分法”可简化运算。
(5)有关圆锥曲线的对称问题
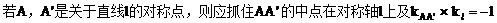
这两个关键条件,同时要记住一些特殊的对称关系,如关于坐标轴对称,关于点对称,关于直线y=±x+b对称。
(6)圆锥曲线中的有关最值问题,常用代数法和几何法解决。
<1>若命题的条件和结论具有明显的几何意义,一般可用图形性质来解决。
<2>若命题的条件和结论体现明确的函数关系式,则可建立目标函数(通常利用二次函数,三角函数,均值不等式)求最值。
[例题选讲]
例1. 已知抛物线y2=2px(p>0)。过动点M(a,0)且斜率为l的直线l与该抛物线交于不同的两点A、B
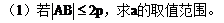
(2)若线段AB的垂直平分线交AB于Q,交x轴于点N,试求三角形MNQ的面积。
解: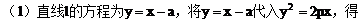
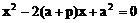
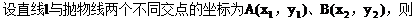
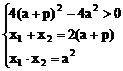
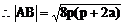
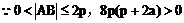
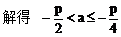
(2)设Q(x3,y3)由中点坐标公式得
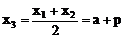
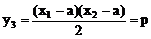
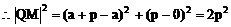
又三角形MNQ为等腰直角三角形
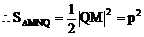
例2. 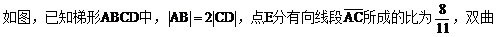 线过C、D、E三点,且以A、B为焦点,求双曲线的离心率。(2000年,全国高考)
线过C、D、E三点,且以A、B为焦点,求双曲线的离心率。(2000年,全国高考)
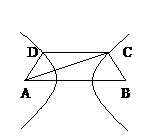
解:以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xOy,则CD⊥y轴,因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称。
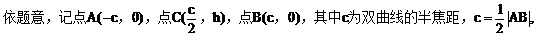
h是梯形的高。
由定比分点坐标公式,得点E的坐标为
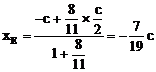
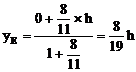

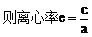
由点C、E在双曲线上,得
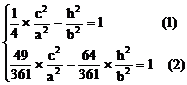
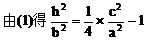
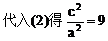
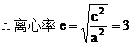
小结:此题涉及解析几何的最根本问题:如何建立坐标系,这也是对学生基本能力的考查,坐标系是一种工具,如果用得好,可以给解题带来方便,但考试时我们不可能对各种情况进行讨论,一般而言,可从对称的角度去考虑。
例3. 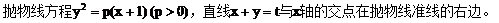
(1)求证:直线与抛物线总有两个不同交点
(2)设直线与抛物线的交点为A、B,且OA⊥OB,求p关于t的函数f(t)的表达式。
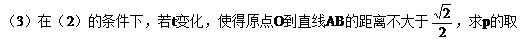 值范围。(1997年.上海高考)
值范围。(1997年.上海高考)
(1)证明:抛物线的准线为
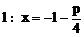
由直线x+y=t与x轴的交点(t,0)在准线右边,得
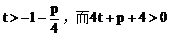
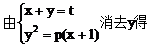
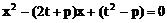
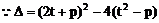
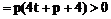
故直线与抛物线总有两个交点。
(2)解:设点A(x1,y1),点B(x2,y2)
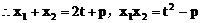
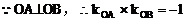
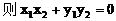
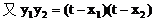
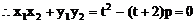
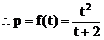
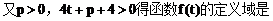
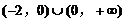
(3)解: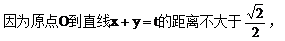
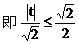
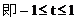
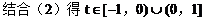
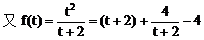
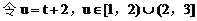
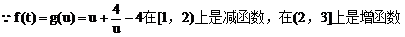
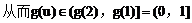
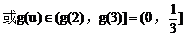
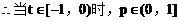
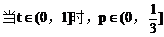
例4. 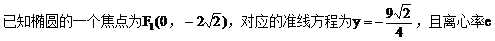

(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线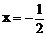 平分,若存在,求出l的倾斜角的范围;若不存在,请说明理由。
平分,若存在,求出l的倾斜角的范围;若不存在,请说明理由。
(1)解: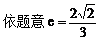
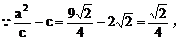
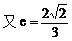
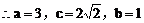
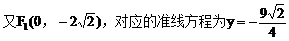

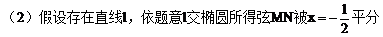
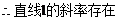
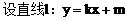
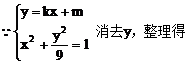

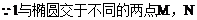
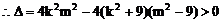
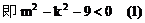
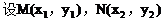
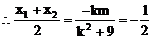
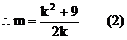
把(2)代入(1)式中得:
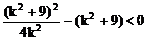
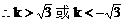
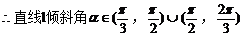
例5. 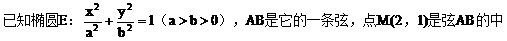 点,若以M(2,1)为焦点,椭圆E的右准线为相应准线的双曲线C和直线AB交于点N(4,-1),且椭圆的离心率e与双曲线离心率e1之间满足ee1=1,
点,若以M(2,1)为焦点,椭圆E的右准线为相应准线的双曲线C和直线AB交于点N(4,-1),且椭圆的离心率e与双曲线离心率e1之间满足ee1=1,
(1)求椭圆E的离心率e;
(2)求双曲线C的方程。
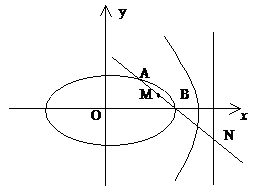
解:(1)因为点M(2,1),点N(4,-1)
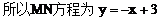
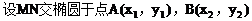
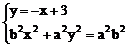
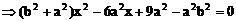
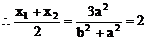
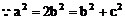
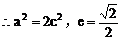
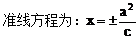
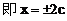
(2)因为ee1=1
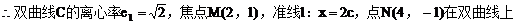
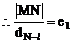
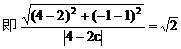
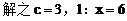
设双曲线C上一点P(x,y)
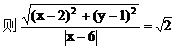
化简得双曲线C的方程:
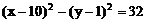
例6. 已知抛物线y2=x上有一条长为l的动弦AB,求AB的中点M到y轴的最短距离。
解:设中点M的坐标为(x,y),利用对称性可设A(x+u,y+v),B(x-u,y-v),依题意有
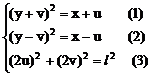
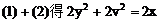
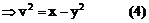

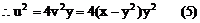
将(4)(5)代入(3)得:
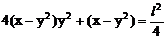
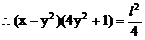
此即M点的方程
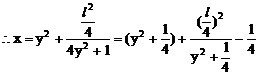
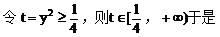
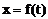
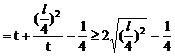
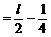
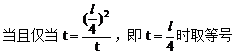

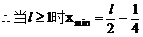
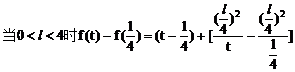
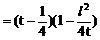
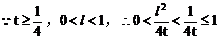
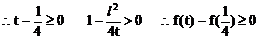

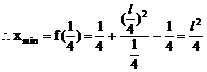
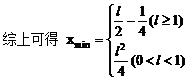
[试题答案]
1. A 2.
C 3. 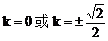 4.
A 5. B 6.
4.
A 5. B 6. 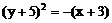
7. C 8. B
9. 证明:(1)令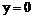 ,得
,得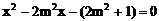
即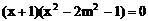
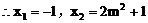
所以抛物线交x轴于定点M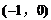
(2)由(1)知,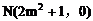 在抛物线方程中
在抛物线方程中
又令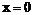 得
得
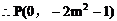
所以直线PN的斜率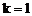 是一个定值。
是一个定值。
(3)由(2)知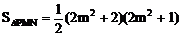
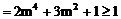
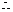 当
当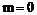 时,
时, 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。