
网址:http://www.1010jiajiao.com/paper/timu/5146166.html[举报]
解析几何的研究对象就是几何图形及其性质,所以在处理解析几何问题时,除了运用代数方程外,充分挖掘几何条件,并结合平面几何知识,这往往能减少计算量。
例1. 已知直线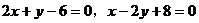 及
及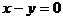 ,求它们所围成的三角形的外接圆方程。
,求它们所围成的三角形的外接圆方程。
解:由直线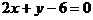 与
与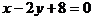 的斜率分别为
的斜率分别为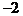 和
和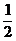 ,得此两条直线互相垂直,即此三角形为直角三角形。
,得此两条直线互相垂直,即此三角形为直角三角形。
由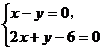 及
及 ,可求得直角三角形的斜边所在的两个顶点分别为
,可求得直角三角形的斜边所在的两个顶点分别为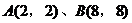 。所求三角形的外接圆,即为以A(2,2)和B(8,8)为直径端点的圆,其方程为
。所求三角形的外接圆,即为以A(2,2)和B(8,8)为直径端点的圆,其方程为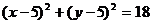
评注:此题若不首先利用三角形是直角三角形这一中间结论,而先求三角形的三个顶点,再解三元一次方程组求圆的一般方程,将会大大增加计算量。
例2. 已知点P(5,0)和圆O: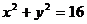 ,过P作直线
,过P作直线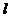 与圆O交于A、B两点,求弦AB中点M的轨迹方程。
与圆O交于A、B两点,求弦AB中点M的轨迹方程。
解: 点M是弦AB中点,
点M是弦AB中点,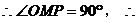 点M是在以OP为直径的圆周上,此圆的圆心为
点M是在以OP为直径的圆周上,此圆的圆心为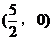 ,半径为
,半径为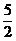 ,所以其方程为
,所以其方程为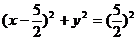 ,即
,即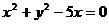 。同时,点M又在圆
。同时,点M又在圆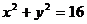 的内部,
的内部,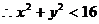 ,即
,即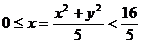 ,所以所求的轨迹方程为
,所以所求的轨迹方程为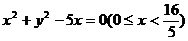
评注:此题若不能挖掘利用几何条件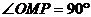 ,点M是在以OP为直径的圆周上,而利用参数方程等方法,计算量将很大,并且比较麻烦。
,点M是在以OP为直径的圆周上,而利用参数方程等方法,计算量将很大,并且比较麻烦。
例3. 求与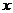 轴相切,圆心在直线
轴相切,圆心在直线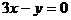 上,且被直线
上,且被直线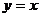 截得的弦长等于
截得的弦长等于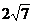 的圆的方程。
的圆的方程。
解:因圆心在直线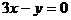 上,故可设圆心
上,故可设圆心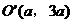
又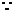 圆与
圆与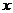 轴相切,
轴相切,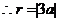 ,
,
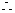 此时可设圆方程为
此时可设圆方程为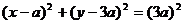
(运用已知条件,找出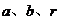 间联系,尽可能把未知量的个数减少,这对简化计算很有帮助。)
间联系,尽可能把未知量的个数减少,这对简化计算很有帮助。)
又圆被直线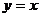 截得的弦长为
截得的弦长为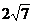 。考虑由圆半径、半弦、弦心距组成的直角三角形,只要将弦心距用
。考虑由圆半径、半弦、弦心距组成的直角三角形,只要将弦心距用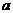 表示出来,便可利用勾股定理求得
表示出来,便可利用勾股定理求得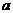 。
。
弦心距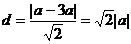
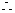
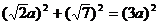 ,解得
,解得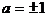
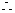 当
当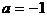 时,
时,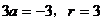 ,圆方程为
,圆方程为
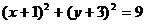
当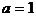 时,
时,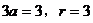 ,圆方程为
,圆方程为
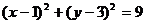
评注:此题若不充分利用圆的半径、半弦、弦心距组成的直角三角形,而用弦长公式,将会增大运算量。
例4. 设直线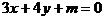 与圆
与圆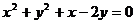 相交于P、Q两点,O为坐标原点,若
相交于P、Q两点,O为坐标原点,若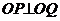 ,求
,求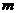 的值。
的值。
解: 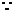 圆
圆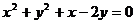 过原点,并且
过原点,并且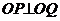 ,
,
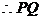 是圆的直径,圆心的坐标为
是圆的直径,圆心的坐标为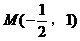
又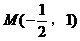 在直线
在直线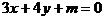 上,
上,
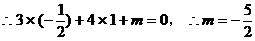 即为所求。
即为所求。
评注:此题若不充分利用一系列几何条件:该圆过原点并且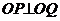 ,PQ是圆的直径,圆心在直线
,PQ是圆的直径,圆心在直线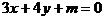 上,而是设
上,而是设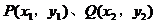 再由
再由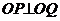 和韦达定理求
和韦达定理求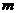 ,将会增大运算量。
,将会增大运算量。
[试题答案]
1. A 2.
C 3. 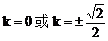 4.
A 5. B 6.
4.
A 5. B 6. 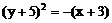
7. C 8. B
9. 证明:(1)令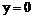 ,得
,得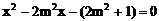
即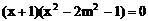
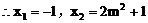
所以抛物线交x轴于定点M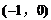
(2)由(1)知,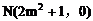 在抛物线方程中
在抛物线方程中
又令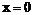 得
得
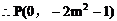
所以直线PN的斜率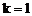 是一个定值。
是一个定值。
(3)由(2)知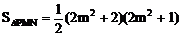
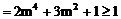
 当
当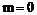 时,
时,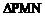 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。