
网址:http://www.1010jiajiao.com/paper/timu/5146167.html[举报]
我们经常设出弦的端点坐标而不求它,而是结合韦达定理求解,这种方法在有关斜率、中点等问题中常常用到。
例5. 已知中心在原点O,焦点在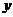 轴上的椭圆与直线
轴上的椭圆与直线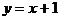 相交于P、Q两点,且
相交于P、Q两点,且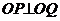 ,
,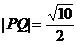 ,求此椭圆方程。
,求此椭圆方程。
解:设椭圆方程为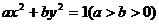 ,直线
,直线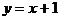 与椭圆相交于P
与椭圆相交于P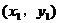 、
、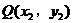 两点。
两点。
由方程组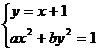 消去
消去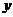 后得
后得
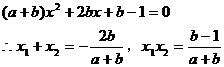
由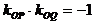 ,得
,得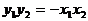 (1)
(1)
又P、Q在直线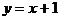 上,
上,
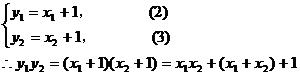
把(1)代入,得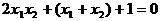 ,
,
即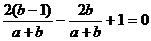
化简后,得
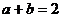 (4)
(4)
由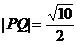 ,得
,得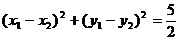
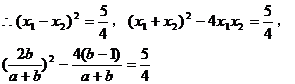
把(2)代入,得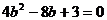 ,解得
,解得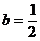 或
或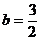
代入(4)后,解得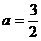 或
或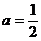
由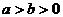 ,得
,得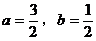 。
。
 所求椭圆方程为
所求椭圆方程为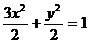
评注:此题充分利用了韦达定理及“设而不求”的策略,简化了计算。
例6. 若双曲线方程为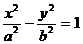 ,AB为不平行于对称轴且不过原点的弦,M为AB中点,设AB、OM的斜率分别为
,AB为不平行于对称轴且不过原点的弦,M为AB中点,设AB、OM的斜率分别为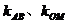 ,则
,则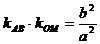
解:设A(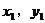 ),B(
),B(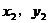 )则M(
)则M(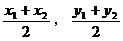 )
)
又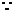 A、B分别在
A、B分别在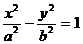 上,则有
上,则有
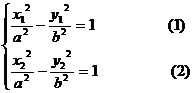
由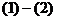 得
得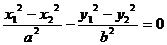 ,
,
即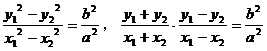 ,
,
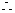
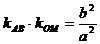
评注:此题充分利用了中点坐标公式斜率公式及“设而不求”的策略,简化了计算。
[试题答案]
1. A 2.
C 3. 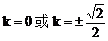 4.
A 5. B 6.
4.
A 5. B 6. 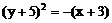
7. C 8. B
9. 证明:(1)令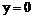 ,得
,得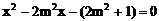
即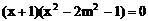
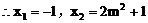
所以抛物线交x轴于定点M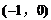
(2)由(1)知,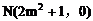 在抛物线方程中
在抛物线方程中
又令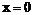 得
得
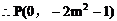
所以直线PN的斜率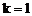 是一个定值。
是一个定值。
(3)由(2)知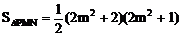
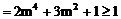
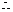 当
当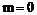 时,
时,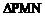 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。