
网址:http://www.1010jiajiao.com/paper/timu/5146180.html[举报]
2.曲线的形状未知-----求轨迹方程
例3 (1994年全国)
 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,
动点M到圆C的切线长与|MQ|的比等于常数
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,
动点M到圆C的切线长与|MQ|的比等于常数 (
( >0),求动点M的轨迹方程,并说明它是什么曲线。
>0),求动点M的轨迹方程,并说明它是什么曲线。
分析:如图,设MN切圆C于点N,则动点M组成的集合是:
P={M||MN|= |MQ|},由平面几何知识可知:|MN|2=|MO|2-|ON|2=|MO|2-1,将M点坐标代入,可得:(
|MQ|},由平面几何知识可知:|MN|2=|MO|2-|ON|2=|MO|2-1,将M点坐标代入,可得:( 2-1)(x2+y2)-4
2-1)(x2+y2)-4 2x+(1+4
2x+(1+4 2)=0.
2)=0.
当 =1时它表示一条直线;当
=1时它表示一条直线;当 ≠1时,它表示圆。
≠1时,它表示圆。
这种方法叫做直接法。
 例4 (1999年全国)
例4 (1999年全国)
给出定点A(a,0)(a>0)和直线L:x=-1,B是直线L上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系。
分析:设C(x,y),B(-1,b).则直线OB的方程为:y=-bx.由题意:点C到OA、OB的距离相等,且点C在线段AB上,所以
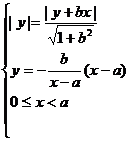
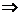 y2[(1-a)x2-2ax+(1+a)y2]=0
y2[(1-a)x2-2ax+(1+a)y2]=0
若,y≠0,则(1-a)x2-2ax+(1+a)y2=0(0<x<a);若y=0,则b=0,∠AOB=180º,点C的坐标为(0,0),也满足上式。所以,点C的轨迹方程为(1-a)x2-2ax+(1+a)y2=0(0≤x<a)。
当a=1时,方程表示抛物线弧;当0<a<1时,方程表示椭圆弧;当a>1时,方程表示双曲线一支的弧。
一般地,如果选择了m个参数,则需要列出m+1个方程。
例5 (1995年全国)
已知椭圆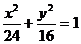 和直线L:
和直线L: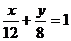 ,P是直线L上一点,射线OP交椭圆于点R,又点Q在OP上,且满足|OQ| |OP|=|OR|2,当点P在L上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线。
,P是直线L上一点,射线OP交椭圆于点R,又点Q在OP上,且满足|OQ| |OP|=|OR|2,当点P在L上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线。
分析:设Q(x,y),P(xP,yP),R(xR,yR), 则
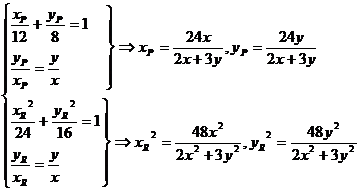 ,代入
,代入
 ,得:
,得: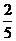 (x-1)2+
(x-1)2+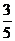 (y-1)2=1.
(y-1)2=1.
注意:若将点P、Q、R分别投影到x轴上,则式子 可用|x| |xP|=|xR2|代替,这样就简单多了。
可用|x| |xP|=|xR2|代替,这样就简单多了。
Ⅱ.研究圆锥曲线有关的问题
[试题答案]
1. A 2.
C 3. 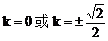 4.
A 5. B 6.
4.
A 5. B 6. 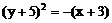
7. C 8. B
9. 证明:(1)令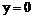 ,得
,得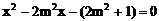
即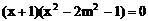
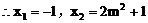
所以抛物线交x轴于定点M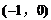
(2)由(1)知,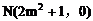 在抛物线方程中
在抛物线方程中
又令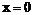 得
得
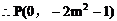
所以直线PN的斜率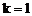 是一个定值。
是一个定值。
(3)由(2)知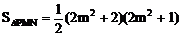
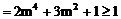
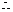 当
当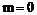 时,
时,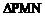 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。