
网址:http://www.1010jiajiao.com/paper/timu/5146191.html[举报]
14. (03年上海)设集合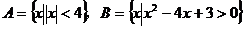 ,则集合
,则集合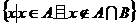 =__________________。
=__________________。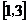
15(03年上海) 给出问题: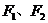 是双曲线
是双曲线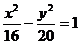 的焦点,点P在双曲线上。若点P到焦点F1的距离等于9,求点P到焦点F2的距离。某学生的解答如下:双曲线的实轴长为8,由
的焦点,点P在双曲线上。若点P到焦点F1的距离等于9,求点P到焦点F2的距离。某学生的解答如下:双曲线的实轴长为8,由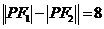 ,即
,即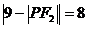 ,得
,得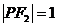 或17。
或17。
该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内;若不正确,将正确结果填在下面空格内。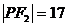
16(03年上海)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分。
如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状。
(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为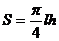 。柱体体积为:底面积乘以高。本题结果均精确到0.1米)
。柱体体积为:底面积乘以高。本题结果均精确到0.1米)

[解](1)如图建立直角坐标系,则点P(11,4.5)
椭圆方程为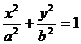
将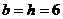 与点P坐标代入椭圆方程,得
与点P坐标代入椭圆方程,得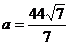 ,此时
,此时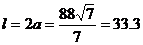
因此隧道的拱宽约为33.3米。
(2)[解一]由椭圆方程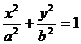
得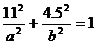
因为 ,即
,即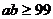 ,且
,且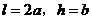
所以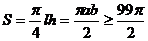
当S取最小值时,有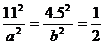 ,得
,得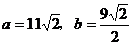
此时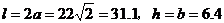
故当拱高约为6.4米,拱宽约为31.1米时,土方工程量最小
[解二]由椭圆方程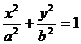 ,得
,得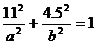
于是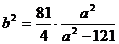

即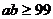 ,当S取最小值时,有
,当S取最小值时,有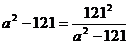
得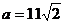 ,
,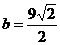 ,以下同解一
,以下同解一
[试题答案]
1. A 2.
C 3. 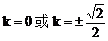 4.
A 5. B 6.
4.
A 5. B 6. 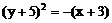
7. C 8. B
9. 证明:(1)令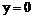 ,得
,得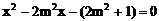
即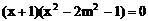
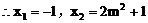
所以抛物线交x轴于定点M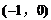
(2)由(1)知,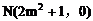 在抛物线方程中
在抛物线方程中
又令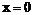 得
得
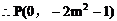
所以直线PN的斜率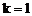 是一个定值。
是一个定值。
(3)由(2)知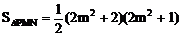
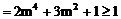
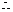 当
当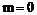 时,
时, 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。