
网址:http://www.1010jiajiao.com/paper/timu/5146192.html[举报]
17. (03年上海)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分7分。
在以O为原点的直角坐标系中,点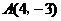 为
为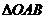 的直角顶点,已知
的直角顶点,已知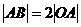 ,且点B的纵坐标大于零。
,且点B的纵坐标大于零。
(1)求向量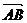 的坐标。
的坐标。
(2)求圆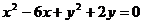 关于直线OB对称的圆的方程。
关于直线OB对称的圆的方程。
(3)是否存在实数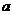 ,使抛物线
,使抛物线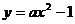 上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求
上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求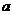 的取值范围。
的取值范围。
解](1)设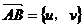 ,则由
,则由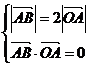 ,即
,即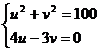 ,得
,得
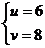 ,或
,或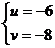
因为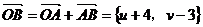
所以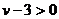 ,得
,得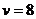 ,故
,故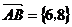
(2)由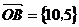 ,得B(10,5),于是直线OB方程:
,得B(10,5),于是直线OB方程: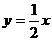
由条件可知圆的标准方程为: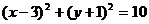
得圆心(3,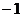 ),半径为
),半径为
设圆心(3,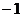 )关于直线OB的对称点为(x,y),则
)关于直线OB的对称点为(x,y),则
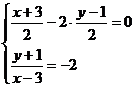 ,得
,得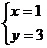
故所求圆的方程为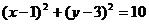
(3)设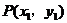 ,
,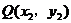 为抛物线上关于直线OB对称的两点,则
为抛物线上关于直线OB对称的两点,则
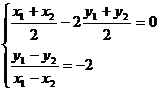 ,得
,得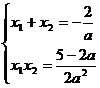
即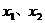 为方程
为方程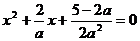 的两个相异实数
的两个相异实数
[试题答案]
1. A 2.
C 3. 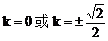 4.
A 5. B 6.
4.
A 5. B 6. 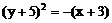
7. C 8. B
9. 证明:(1)令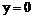 ,得
,得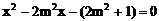
即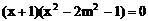
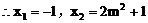
所以抛物线交x轴于定点M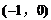
(2)由(1)知,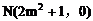 在抛物线方程中
在抛物线方程中
又令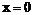 得
得
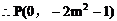
所以直线PN的斜率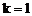 是一个定值。
是一个定值。
(3)由(2)知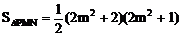
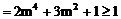
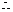 当
当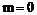 时,
时,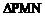 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。