
网址:http://www.1010jiajiao.com/paper/timu/5146195.html[举报]
20.本小题主要考查平面向量的概念和计算,求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程的关系等解析几何的基本思想和综合解题能力,满分14分。
解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
∵i=(1,0),c=(0,a), ∴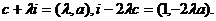
因此,直线OP和AP的方程分别为  y=ax和y-a=-2
y=ax和y-a=-2 ax .
ax .
消去参数 ,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2 ,
,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2 ,
整理得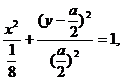 ①
①
因为a>0,所以得:
(i)当a=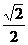 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;
(ii)当0<a<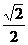 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E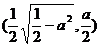 和
和
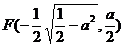 为合乎题意的两个定点;
为合乎题意的两个定点;
(iii)当a>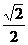 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E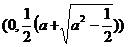 和F
和F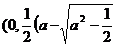 ))为合乎题意的两个定点.
))为合乎题意的两个定点.
[试题答案]
1. A 2.
C 3. 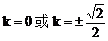 4.
A 5. B 6.
4.
A 5. B 6. 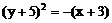
7. C 8. B
9. 证明:(1)令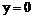 ,得
,得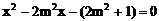
即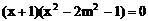
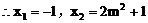
所以抛物线交x轴于定点M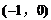
(2)由(1)知,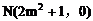 在抛物线方程中
在抛物线方程中
又令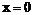 得
得
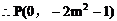
所以直线PN的斜率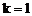 是一个定值。
是一个定值。
(3)由(2)知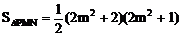
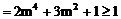
 当
当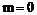 时,
时,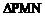 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。