
网址:http://www.1010jiajiao.com/paper/timu/5146201.html[举报]
21.根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在的两定点,使得点P到两点距离的和为定值.
按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a)设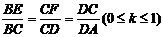
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak)直线OF的方程为: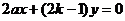 ①
①
直线GE的方程为: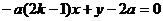 ②
②
从①,②消去参数k,得点P(x,y)坐标满足方程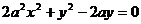
整理得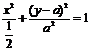 当
当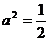 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当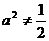 时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长。
当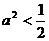 时,点P到椭圆两个焦点(
时,点P到椭圆两个焦点(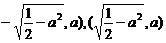 的距离之和为定值
的距离之和为定值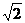 。
。
当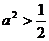 时,点P 到椭圆两个焦点(0,
时,点P 到椭圆两个焦点(0,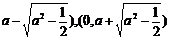 的距离之和为定值2
的距离之和为定值2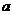 .
.
[模拟试题]
[试题答案]
1. A 2.
C 3. 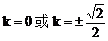 4.
A 5. B 6.
4.
A 5. B 6. 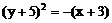
7. C 8. B
9. 证明:(1)令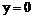 ,得
,得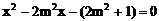
即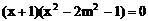
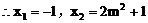
所以抛物线交x轴于定点M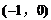
(2)由(1)知,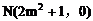 在抛物线方程中
在抛物线方程中
又令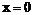 得
得
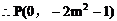
所以直线PN的斜率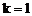 是一个定值。
是一个定值。
(3)由(2)知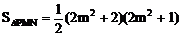
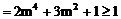
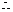 当
当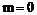 时,
时, 的面积最小,其最小面积为1。
的面积最小,其最小面积为1。