
网址:http://www.1010jiajiao.com/paper/timu/5146215.html[举报]
[例1] 已知数列{an}、{bn}都是等差数列,a1=0、b1= -4,用Sk、S′k、分别表示数列{an}、{bn}的前k项和(k是正整数),若Sk+S′k =0,则ak+bk的值为 。
[解] 法一 直接应用等差数列求和公式Sk= ,得
,得 +
+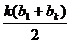 =0,又a1+b1= -4, ∴ak+bk=4。
=0,又a1+b1= -4, ∴ak+bk=4。
法二 由题意可取k=2(注意:k≠1,为什么?),于是有a1+a2+b1+b2=0,因而a2+b2=4,即ak+bk=4。
[例2] 乒乓球队的10名队员中有3名主力队员,派5名参加比赛。3名主力队员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四位置,那么不同的出场安排共有 种(用数字作答)。
[解] 三名主力队员的排法有P33种,其余7名队员选2名安排在第二、四位置上有P72种排法,故共有排法数A33A72=252种。
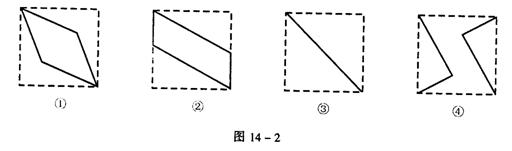
[例3] 如图14-1,E、F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 (要求:把可能的图的序号都填上)。
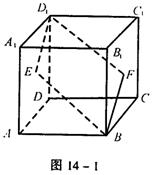
[解] 正方体共有3 组对面,分别考察如下:(1)四边形BFD1E在左右一组面上的射影是图③。因为B点、F点在面AD1上的射影分别是A点、E点。(2)四边形BFD1E在上下及前后两组面上的射影是图②。因为D1点、E点、F点在面AC上的射影分别是D点、AD中点、BC中点;B点、E点、F点在面DC1上的射影分别是C点、DD1的中点、CC1的中点。故本题答案为②③。
[例4] 已知抛物线的焦点坐标为F(2,1),准线方程为2x+y=0,则其顶点坐标为 。
[解] 过焦点F(2,1)作准线的垂线段,由解几何知识可得抛物线顶点为垂线段的中点。又由于准线的斜率k= -2,kOF=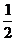 ,∴O为垂足,从而易得OF的中点,即顶点为(1,
,∴O为垂足,从而易得OF的中点,即顶点为(1, 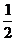 )。
)。
[例5] 老师给出一个函数y=f(x),四个学生甲、乙、丙、丁各指出这个函数的一个性质:
甲:对于x∈R,都有f(1+x)=f(1-x) 乙:在 (-∞,0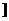 上函数递减
上函数递减
丙:在(0,+∞)上函数递增 丁:f(0)不是函数的最小值
如果其中恰有三人说得正确,请写出一个这样的函数 。
[解] 由题意知,以甲、乙、丙、丁四个条件中任意三个为一组条件,写出符合条件的一个函数最可。例如同时具备条件甲、乙、丁的一个函数为y=(x-1)2。
[例6]
若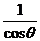 -
-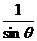 =1,则sin2θ的值等于 。
=1,则sin2θ的值等于 。
[解] 由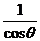 -
-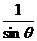 =1得sinθ-cosθ=sinθcosθ ①
=1得sinθ-cosθ=sinθcosθ ①
令sin2θ=t,则①式两边平方整理得t2+4t-4=0,解之得t=2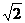 -2。
-2。
[例7]
已知z1=3+4i,z2=
-2-5i,则arg(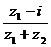 )= 。
)= 。
[解] 将z1=3+4i,z2=
-2-5i代入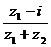 整理得
整理得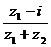 =3i,故arg(
=3i,故arg(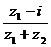 )=
)=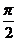 。
。
[例8]
若(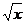 +
+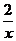 )n展开式中的第5项为常数,则n= 。
)n展开式中的第5项为常数,则n= 。
[解] 由Tr+1=Cnr(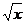 )n-r(
)n-r(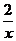 )r=Cnr2rx
)r=Cnr2rx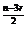 及题意可知,当r=4时,n-3r=0,∴n=12。
及题意可知,当r=4时,n-3r=0,∴n=12。

参考答案
1.75 2.  3.1800 4.
3.1800 4. 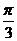 5.12 6.1680 7.
5.12 6.1680 7.
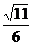 8.3
9.g(2),g(5),g(-2 )10.-10 11.2
8.3
9.g(2),g(5),g(-2 )10.-10 11.2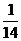 12.2.6 13.
12.2.6 13. 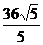 14.
14. 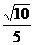 15.m-p 16. π 17.(3,-
15.m-p 16. π 17.(3,- 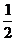 ) 18.-8 19.12
20.{x|-2<x<1} 21.20 22.a∥b
) 18.-8 19.12
20.{x|-2<x<1} 21.20 22.a∥b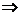 c∥d 23.(0,2
c∥d 23.(0,2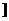 24. -
24. -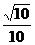 25.2
25.2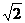 26.
26. 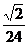 、
、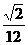 、
、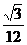 27.
27. 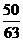 28.①②⑤ 29.-
28.①②⑤ 29.- 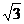 30.
30. 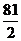 31.6
31.6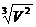 32. ④②①③ 33.
32. ④②①③ 33. 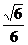 34.x=0或15x+8y-32=0 35.
34.x=0或15x+8y-32=0 35.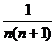 36.(1) ①③
36.(1) ①③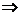 ②④ (2) ②③
②④ (2) ②③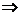 ①④ 37.X= -
①④ 37.X= -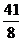 38.
38.  39.
39. 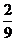 40.5对 41.截面AB1D1,或截面ACD1,或截面AB1C 42.
40.5对 41.截面AB1D1,或截面ACD1,或截面AB1C 42. 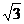 x-3y-
x-3y-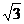 =0(或)
=0(或)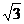 x+3y-
x+3y-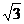 =0 43.
=0 43. 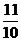 44.arccos
44.arccos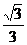 45.-
45.- 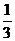 46.(x-1)2+(y±2
46.(x-1)2+(y±2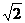 )2=9 47. ∠ABD>90°(或∠ACD>90°)或∠BAD+∠ADB<90°,或∠ADC+∠CAD<90°) 48. ③④ 49.y=-
)2=9 47. ∠ABD>90°(或∠ACD>90°)或∠BAD+∠ADB<90°,或∠ADC+∠CAD<90°) 48. ③④ 49.y=-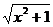 (x≥0)
(x≥0)