
网址:http://www.1010jiajiao.com/paper/timu/5146347.html[举报]
一项是符合题目要求的.
1.下列不等式的在区间(0,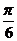 )内恒成立的是 ( )
)内恒成立的是 ( )
A.sinx>cosx B.tanx>cotx C.cosx>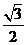 D.sinx>
D.sinx>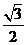
综合测试题(1)参考答案
一、选择题
1.C 2.D 3.C 4.D 5.C 6.A. 7.A 8.D 9.C 10.B 11.C 12.C
二、填空题
13. 8 14. 14 15. 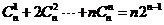 16. 54
16. 54
三、解答题
17.(I)由题意a+b=(cosα+cosβ, sinα+sinβ), a-b=(cosα-cosβ, sinα-sinβ)
∵(a+b).(a-b)= (cosα+cosβ)(cosα-cosβ)+(sinα+sinβ)(sinα-sinβ)
= cos2α-cos2β+ sin2α-sin2β=1-1=0
∴a+b 与a-b互相垂直.
(II) ka+b=(kcosα+cosβ,ksinα+sinβ), a-kb=(cosα-kcosβ, sinα-ksinβ)
|ka+b|=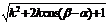 , |a-kb|=
, |a-kb|=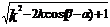
由题意,得4cos(β-α)=0, 因为0<α<β<π
,所以β-α=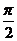
18.(I)以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系. ∵AC=2a,∠ABC=90º. ∴AB=BC=a. 从而B(0,0,0),A(a,0,0),C(0,a,0), A1(a,0,3a),B1(0,0,3a),C1(0,a,3a), D(,3a),E(0,).………………2分 ∴). 而 . ………4分 ∴cosθ= ∴θ=arctan …………6分 (II)设AF=x,则F( a,0,x) …………7分 +x×0=0 ∴……………10分 要使得CF⊥平面B1DF,只需CF⊥B1F ,由=2a2+x(x-3a)=0 有x=a或x=2a 故当AF=a,或AF=2a时,CF⊥平面B1DF.…………………12分
 19.⑴由题意,存款量g(x)=kx2,银行应支付的利息h(x)=x.g(x)=kx3 . ……4分
19.⑴由题意,存款量g(x)=kx2,银行应支付的利息h(x)=x.g(x)=kx3 . ……4分
⑵设银行可获收益为y, 则y=0.048.kx2- kx3 ;
y/=0.096.kx-3kx2 …………………6分
令y/=0即0.096.kx-3kx2=0 解得x=0或x=0.032
又当x∈(0,0.032)时 , y/>0,当 x∈(0.032,0.048)时,y/<0. ………8分
∴y在(0,0.032)内单调递增,在(0.032,0.048)内单调递减;
故当x=0.032时, y在(0,0.048)内取得极大值,也是最大值.
故存款的利率为3.2%,银行可获得最大收益. ………………12分
20.设船速为v,显然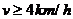 时人是不可能追上小船,当
时人是不可能追上小船,当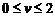 km/h时,人不必在岸上跑,而只要立即从同一地点直接下水就可以追上小船,因此只要考虑
km/h时,人不必在岸上跑,而只要立即从同一地点直接下水就可以追上小船,因此只要考虑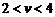 的情况,由于人在水中游的速度小于船的速度,人只有先沿湖岸跑一段路后再游水追赶,当人沿岸跑的轨迹和人游水的轨迹以及船在水中漂流的轨迹组成一个封闭的三角形时,人才能追上小船.设船速为v,人追上船所用时间为t,人在岸上跑的时间为
的情况,由于人在水中游的速度小于船的速度,人只有先沿湖岸跑一段路后再游水追赶,当人沿岸跑的轨迹和人游水的轨迹以及船在水中漂流的轨迹组成一个封闭的三角形时,人才能追上小船.设船速为v,人追上船所用时间为t,人在岸上跑的时间为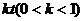 ,则人在水中游的时间为
,则人在水中游的时间为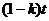 ,人要追上小船,则人船运动的路线满足如图所示的三角形.……………4分
,人要追上小船,则人船运动的路线满足如图所示的三角形.……………4分
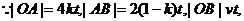 由余弦是理得
由余弦是理得
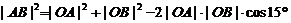 ………………6分
………………6分
即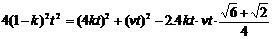
整理得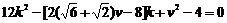 .
………………8分
.
………………8分
要使上式在(0,1)范围内有实数解,则有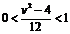 且
且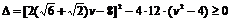
解得 .
………………10分
.
………………10分
故当船速在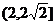 内时,人船运动路线可物成三角形,即人能追上小船,船能使人追上的最大速度为
内时,人船运动路线可物成三角形,即人能追上小船,船能使人追上的最大速度为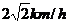 ,由此可见当船速为2.5km/h时, 人可以追上小船.…………12分
,由此可见当船速为2.5km/h时, 人可以追上小船.…………12分
21.⑴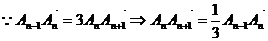
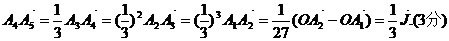
⑵由⑴知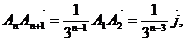
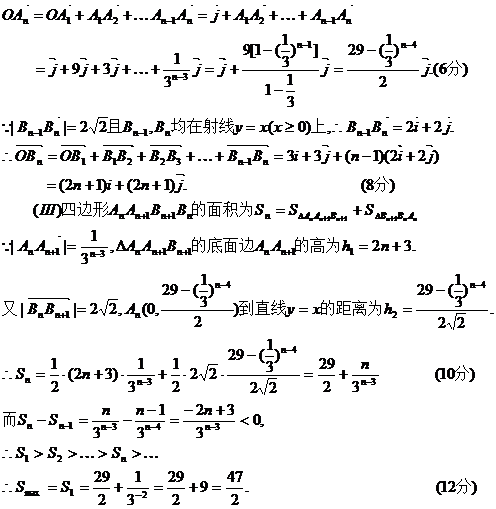
22.⑴ 依题意有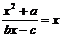 ,化简为
,化简为 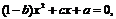 由违达定理, 得
由违达定理, 得 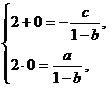
解得
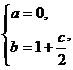 ……………2分
……………2分
代入表达式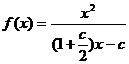 ,由
,由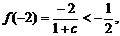
得 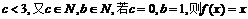 不止有两个不动点,
不止有两个不动点,
 ………………4分
………………4分
⑵由题设得 (*)
(*)
且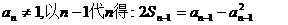 (**)
(**)
………………6分
由(*)与(**)两式相减得:
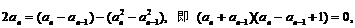
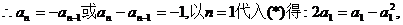
解得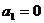 (舍去)或
(舍去)或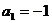 ,由
,由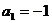 ,若
,若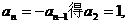 这与
这与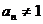 矛盾,
矛盾,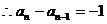 ,即{
,即{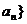 是以-1为首项,-1为公差的等差数列,
是以-1为首项,-1为公差的等差数列,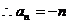 .
……9分
.
……9分
⑶采用反证法,假设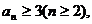 则由(I)知
则由(I)知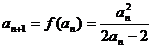
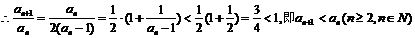 ,
,
有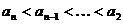 ,而当
,而当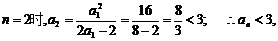
这与假设矛盾,故假设不成立. ∴an<3 ……………14分