
网址:http://www.1010jiajiao.com/paper/timu/5146371.html[举报]
3.设m、n是两条不同的直线,a,b,g是三个不同的平面,给出下列四个命题:
①若m⊥a,n∥a,则m⊥n ②若a∥b,b∥g,m⊥a,则m⊥g
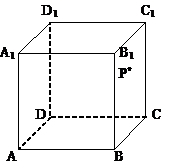 ③若m∥a,n∥a,则m∥n
④若a⊥g,b⊥g,则a∥b
③若m∥a,n∥a,则m∥n
④若a⊥g,b⊥g,则a∥b
其中正确命题的序号是( )
A.①和② B.②和③
C. ③和④ D.①和④
开放与探索水平测试参考答案
一. 选择题:本大题主要考查基本知识和基本运算。每小题5分,满分60分。
1.A 2.C 3.A 4.D 5.D 6.C 7.B 8.B 9.A 10.A 11.C 12.B
二. 填空题:本大题主要考查基本知识和基本运算。每小题4分,满分16分。
13.②④ 14.①④ 15.用代数的方法研究图形的几何性质.
16.3 当n为偶数时,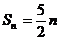 ;当n为奇数时,
;当n为奇数时,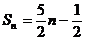
三. 解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.思路点拨:解答时首先应该读懂题意,不必深究这到底是一个什么变换,是否存在这样的直线其实质就是(x,y)与(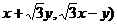 两点是否均在同一直线上,从而转换为讨论方程组的解的问题。
两点是否均在同一直线上,从而转换为讨论方程组的解的问题。
详细解答:假设存在这样的直线,∵平行于坐标轴的直线显然不符合条件,故可设所求的直线方程为y=kx+b(k≠0)该直线上任何一点(x,y)经过变换后得到点(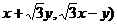 仍旧在该直线上。∴
仍旧在该直线上。∴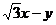 =k(
=k(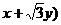 +b,也就是
+b,也就是
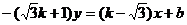 ,∵
,∵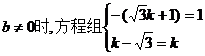 无解,故不存在这样的直线。
无解,故不存在这样的直线。
当b=0时由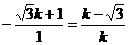 ,解得k=
,解得k=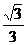 或k=
或k=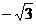 ,所以满足条件的所有直线为y=
,所以满足条件的所有直线为y=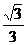 x或y=
x或y=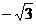 x。
x。
18.解:⑴f'(x)=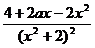 =
= 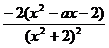 ,
,
∵f(x)在[-1,1]上是增函数,
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立. ①
设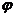 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:①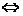
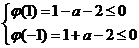
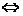 -1≤a≤1,
-1≤a≤1,
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f ′(-1)=0以及当a=-1时,f ′(1)=0
∴A={a|-1≤a≤1}.
方法二:①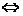
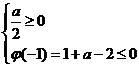 或
或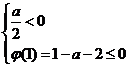
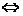 0≤a≤1或-1≤a<0
0≤a≤1或-1≤a<0
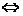 -1≤a≤1.
-1≤a≤1.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
⑵由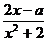 =
= ,得x2-ax-2=0, ∵△=a2+8>0
,得x2-ax-2=0, ∵△=a2+8>0
∴x1,x2是方程x2-ax-2=0的两实根,∴ 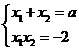
从而|x1-x2|=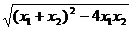 =
=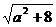 .
.
∵-1≤a≤1,∴|x1-x2|=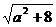 ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立. ②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:②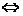
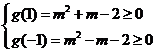
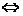 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二: 当m=0时,②显然不成立; 当m≠0时,
②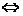
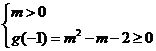 或
或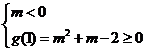
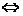 m≥2或m≤-2.
m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
19.解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得点P到两定点距离的和为定值.
∵i=(1,0),c=(0,a),
∴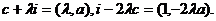
因此,直线OP和AP的方程分别为
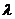 y=ax和y-a=-2
y=ax和y-a=-2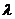 ax .
ax .
消去参数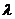 ,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2 ,
,得点P(x,y)的坐标满足方程y (y-a)=-2a2x2 ,
整理得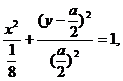 ①
①
因为a>0,所以得:
(i)当a=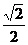 时,方程①是圆方程,故不存在合乎题意的定点E和F;
时,方程①是圆方程,故不存在合乎题意的定点E和F;
(ii)当0<a<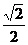 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E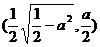 和
和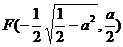
为合乎题意的两个定点;
(iii)当a>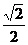 时,方程①表示椭圆,焦点E
时,方程①表示椭圆,焦点E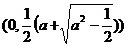 和F
和F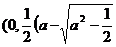 ))为合乎题意的两个定点.
))为合乎题意的两个定点.
20.解:⑴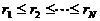 。除第N组外的每组至少含有
。除第N组外的每组至少含有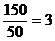 个数
个数
⑵当第n组形成后,因为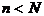 ,所以还有数没分完,这时余下的每个数必大于余差
,所以还有数没分完,这时余下的每个数必大于余差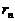 ,余下数之和也大于第n组的余差
,余下数之和也大于第n组的余差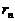 ,即
,即
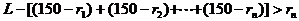
由此可得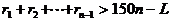
因为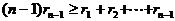 ,所以
,所以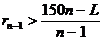
⑶用反证法证明结论,假设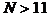 ,即第11组形成后,还有数没分完,由(I)和(II)可知,余下的每个数都大于第11组的余差
,即第11组形成后,还有数没分完,由(I)和(II)可知,余下的每个数都大于第11组的余差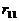 ,且
,且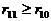
故余下的每个数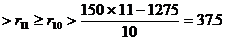 (*)
(*)
因为第11组数中至少含有3个数,所以第11组数之和大于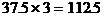
此时第11组的余差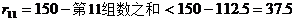
这与(*)式中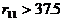 矛盾,所以
矛盾,所以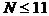
21.(1) a1=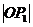 2=100,由S3=
2=100,由S3=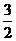 (a1+a3)=255,得a3=
(a1+a3)=255,得a3=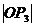 3=70.
3=70.
由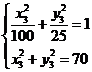 得
得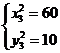
∴点P3的坐标可以为(2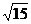 ,
, 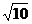 ).
).
(2) [解法一]原点O到二次曲线C: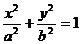 (a>b>0)上各点的最小距离为b,最大距离为a.
(a>b>0)上各点的最小距离为b,最大距离为a.
∵a1=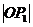 2=a2,
∴d<0,且an=
2=a2,
∴d<0,且an=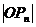 2=a2+(n-1)d≥b2,
2=a2+(n-1)d≥b2,
∴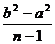 ≤d<0. ∵n≥3,
≤d<0. ∵n≥3,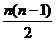 >0
>0
∴Sn=na2+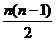 d在[
d在[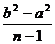 ,0)上递增,
,0)上递增,
故Sn的最小值为na2+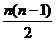 .
.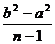 =
=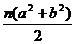 .
.
[解法二]对每个自然数k(2≤k≤n),
由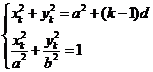 解得y
解得y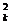 =
=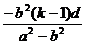
∵0< y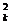 ≤b2,得
≤b2,得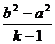 ≤d<0
≤d<0
∴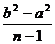 ≤d<0
≤d<0
以下与解法一相同.
(3) [解法一]若双曲线C: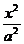 -
-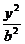 =1,点P1(a,0),
=1,点P1(a,0),
则对于给定的n, 点P1, P2,…Pn存在的充要条件是d>0.
∵原点O到双曲线C上各点的距离h∈[|a|,+∞),且|OP1|=a2,
∴点P1, P2,…Pn存在当且仅当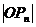 2>
2>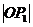 2,即d>0.
2,即d>0.
[解法二]若抛物线C:y2=2x,点P1(0,0),
则对于给定的n, 点P1, P2,…Pn存在的充要条件是d>0.理由同上
[解法三]若圆C:(x-a)+y2=a2(a≠0), P1(0,0),
则对于给定的n, 点P1,
P2,…Pn存在的充要条件是0<d≤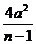 .
.
∵原点O到圆C上各点的最小距离为0,最大距离为2|a|,
且|OP1|=0, ∴d>0且|OPn|2=(n-1)d≤4a2.即0<d≤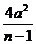 .
.
22.解:⑴如图1,沿正三角形三边中点连线折起,可拼得一个正三棱锥.
如图2,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的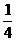 ,有一组对角为直角.余下部分按虚线折起,可成为一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱柱的上底.
,有一组对角为直角.余下部分按虚线折起,可成为一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱柱的上底.
⑵依上面剪拼的方法,有V柱>V锥.
推理如下:
设给出正三角形纸片的边长为2,那么,正三棱锥与正三棱柱的底面都是边长为1的正三角形,其面积为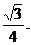 现在计算它们的高:
现在计算它们的高:
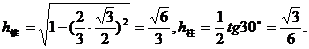
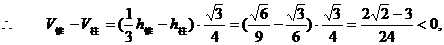
所以,V柱>V锥.
⑶如图3,分别连结三角形的内心与各顶点,得到三条线段,再以这三条线段的中点为顶点作三角形.以新作的三角形为直三棱柱的底面,过新三角形的三个顶点向原三角形三边作垂线,沿六条垂线剪下三个四边形,可以拼接成直三棱柱的上底,余下部分按虚线折起,成为一个缺上底的直三棱柱,即可得到直三棱柱模型.
|