网址：http://www.1010jiajiao.com/paper/timu/5146407.html[举报]
从新教材开始的新高考命题统计看(见下表),对向量与三角的考查立足于基础题和中档题.位置一般在选择的前位和解答题的前三个.
04年全国14套试卷每一套解答题的第一题都是有关三角或向量,不是三角求值,就是三角函数,或向量与三角相结合.而小题主要是三角函数图象性质,或是利用诱导公式与倍角公式进行三角变形求值.但新教材与老教材最明显的区别就在于降低了三角变形要求.这在新高考中得到了充分的体现.
如03年江苏卷19题已知函数f(x)=sin(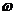
x+
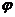
)是R上的偶函数,其图象关于点(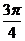
,0)对称,且在区间[0,
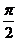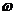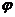]上是单调函数,求和的值
03新课程理17已知函数f(x)=2sinx(sinx+cosx)
Ⅰ、求函数f(x)的最小正周期和最大值
Ⅱ、在给出的坐标系中画出函数y=f(x)在区间[o,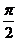]上的图象
(04天津17题)已知tan(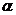
+
)=
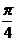Ⅰ、求tan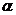值
Ⅱ、求
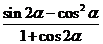的值
(04江苏17题)已知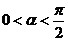
,
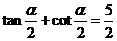,求
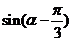的值.
以上考题,都表明了删除繁杂的三角变形,但三角公式还是要熟练的.如江苏17题若不知半角的切公式,应用常规的切化弦亦可以.从江苏03年的第19题可知对三角函数的要求却远远超出考纲中的了解.
向量是新增内容,从新高考命题思路看,主要是把向量作为工具与三角或解几立几相结合进行考查.或在小题中对向量的概念基本运算进行考查.命题的重点在向量的坐标式与向量的几何形式与向量的矢量式三种.
如去年(湖北的第19题)如图在Rt△ABC中, 已知BC=a,若长为2a的线段PQ以点A为中点,问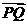
与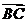
的夹角取何值时, 
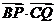的值最大并求出这个最大值.
(江苏16题)平面向量a,b中,已知a=(4,-3),|b|=1,且a•b=5则向量b.
这些考题说明对向量的要求围绕考纲要求设计考题.但向量的三种形式进行了全方位的考查.因此对向量的复习要围绕考纲进行设计试题.
|
|
2004年全理 |
2004全新理 |
2004天津 |
2004江苏 |
2003年新江苏 |
|
选择题 |
3(向量)、9(图象) |
5(切图象)、9(向量数量积)、10、11(周期) |
3(向量)、9(三角单调性)、12(周期应用) |
2 |
|
|
填空题 |
|
|
|
16(向量) |
|
|
解答题 |
17三角变形求值 |
17解三角形 |
17求值22向量与解几 |
17三角求值 |
|