网址:http://www.1010jiajiao.com/paper/timu/5146692.html[举报]
例1、已知集合M={y|y=x2+1,x∈R},N={y|y=x+1,x∈R},求M∩N。
解题思路分析:
在集合运算之前,首先要识别集合,即认清集合中元素的特征。M、N均为数集,不能误认为是点集,从而解方程组。其次要化简集合,或者说使集合的特征明朗化。M={y|y=x2+1,x∈R}={y|y≥1},N={y|y=x+1,x∈R}={y|y∈R}
∴ M∩N=M={y|y≥1}
说明:实际上,从函数角度看,本题中的M,N分别是二次函数和一次函数的值域。一般地,集合{y|y=f(x),x∈A}应看成是函数y=f(x)的值域,通过求函数值域化简集合。此集合与集合{(x,y)|y=x2+1,x∈R}是有本质差异的,后者是点集,表示抛物线y=x2+1上的所有点,属于图形范畴。集合中元素特征与代表元素的字母无关,例{y|y≥1}={x|x≥1}。
例2、已知集合A={x|x2-3x+2=0},B+{x|x2-mx+2=0},且A∩B=B,求实数m范围。
解题思路分析:
化简条件得A={1,2},A∩B=B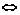 B
B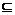 A
A
根据集合中元素个数集合B分类讨论,B=φ,B={1}或{2},B={1,2}
当B=φ时,△=m2-8<0
∴ 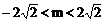
当B={1}或{2}时,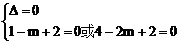 ,m无解
,m无解
当B={1,2}时,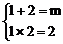
∴ m=3
综上所述,m=3或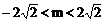
说明:分类讨论是中学数学的重要思想,全面地挖掘题中隐藏条件是解题素质的一个重要方面,如本题当B={1}或{2}时,不能遗漏△=0。
例3、用反证法证明:已知x、y∈R,x+y≥2,求 证x、y中至少有一个大于1。
解题思路分析:
假设x<1且y<1,由不等式同向相加的性质x+y<2与已知x+y≥2矛盾
∴ 假设不成立
∴ x、y中至少有一个大于1
说明;反证法的理论依据是:欲证“若p则q”为真,先证“若p则非q”为假,因在条件p下,q与非q是对立事件(不能同时成立,但必有一个成立),所以当“若p则非q”为假时,“若p则q”一定为真。
例4、若A是B的必要而不充分条件,C是B的充要条件,D是C的充分而不必要条件,判断D是A的什么条件。
解题思路分析:
利用“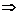 ”、“
”、“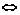 ”符号分析各命题之间的关系
”符号分析各命题之间的关系
D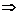 C
C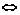 B
B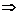 A
A
∴ D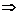 A,D是A的充分不必要条件
A,D是A的充分不必要条件
说明:符号“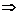 ”、“
”、“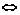 ”具有传递性,不过前者是单方向的,后者是双方向的。
”具有传递性,不过前者是单方向的,后者是双方向的。
例5、求直线:ax-y+b=0经过两直线1:2x-2y-3=0和2:3x-5y+1=0交点的充要条件。
解题思路分析:
从必要性着手,分充分性和必要性两方面证明。
由  得1,2交点P(
得1,2交点P(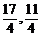 )
)
∵ 过点P
∴ 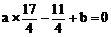
∴ 17a+4b=11
充分性:设a,b满足17a+4b=11
∴ 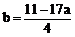
代入方程: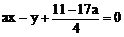
整理得: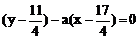
此方程表明,直线恒过两直线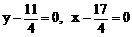 的交点(
的交点(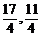 )
)
而此点为1与2的交点
∴ 充分性得证
∴ 综上所述,命题为真
说明:关于充要条件的证明,一般有两种方式,一种是利用“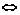 ”,双向传输,同时证明充分性及必要性;另一种是分别证明必要性及充分性,从必要性着手,再检验充分性。
”,双向传输,同时证明充分性及必要性;另一种是分别证明必要性及充分性,从必要性着手,再检验充分性。
参考答案
(一) 选择题
1、C 2、A 3、C 4、C 5、D 6、B 7、B 8、C 9、D 10、A
(二) 填空题
11、φ 12、25,60 13、-1≤a≤1 14、若a、b均不为0,则ab≠0 15、7
(三) 解答题
16、a≥1或a≤-1,提示:画图
17、 3<m≤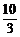
18、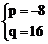 ,或
,或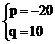 ,或
,或