网址：http://www.1010jiajiao.com/paper/timu/5146727.html[举报]
4、概率密度曲线是某一函数的图象，其中最重要最常见的是正态分布函数。
正态分布函数的解析式：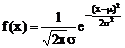
，x∈(-∞，+∞)，其中μ，
(>0)分别表示总体的平均数与标准差，可简记为x-N(μ，2)。此时曲线称为正态曲线：
当μ=0，=1时，称为标准正态分布，简记为x-N(0，1)，分布密度函数用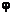
(x)表示，即
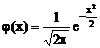，-∞<x<∞。
一般正态分布的问题可以转化为标准正态变量来处理；若ξ-N(μ， 2)，作代换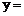
(ξ-μ)/，则ξ-N(0，1)。
参考答案
(一)选择题：
1、C 2、B 3、C 4、B 5、B 6、D 7、D 8、D 9、C 10、C
(二)填空题：
11、x=μ 12、20 13、0.997 14、640 15、16
(三) 解答题：
16、F(60)=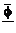
=(-
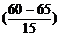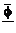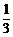)=1-(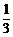)=0.37
∵ 0.37×1500=556
∴ 低于60分的人数为556
17、(1)当x=24时，所抽取样本的10个号码依次为：24，157，290，323，486，589，622，755，888，921；
(2)当k=0，1，2，…，9时，33k的值依据为0，33，60，99，132，165，198，231，264，297
又抽取样本的10个号码中有一个的后两位是87，从而x可以为87，54，21，88，55，22，89，56，23，90
∴ x∈{21，22，23，54，55，56，87，88，89，90}
18、设录取系数为x分，则P(ξ≥x)=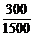
=0.2
∵ ξ-N(75，64)
∴ (ξ-75)/8 -N(0，1)
1- P[(ξ-75)/8 <(x-75)/8]=0.2
即
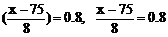
∴ x≈82
19、设y关于x的线性回归方程为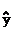
=bx+a，则
Q=[0-(a-b)]2+(0-a)2+(1-a-b)2+(4-2b-a)2=4a2+4ab+6b2-10a-18b+17
=4[a-(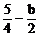
)]2+5(b-
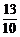)2+
最小
∴ 
∴ 
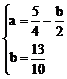
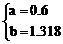
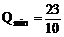
∴ 所求线性回归方程为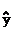=1.3x+0.6
20、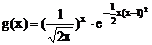
令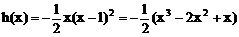
用定义可证明h(x)在(1，+∞)上是减函数
设x2>x1>1，则h(x2)<h(x1)
∴ 
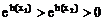
又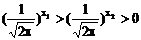 
∴ g(x1)>g(x2) ∴ g(x)在(1，+∞)上是减函数。