
网址:http://www.1010jiajiao.com/paper/timu/5146747.html[举报]
例1、用n种不同颜色为下列两块广告牌着色(如图),要求在①,②,③,④个区域中相邻(有公共边界)的区域不用同一种颜色。
(1)若n=6,为甲着色时共有多少种不同方法?
(2)若为乙着色时共有120种不同方法,求n。
解:完成着色这件事,共分四个步骤,可依次考虑为①、②、③、④着色时各自的方法数,再由乘法原理确定决的着色方法数。因此
(1)为①着色有6种方法,为②着色有5种方法,为③着色有4种方法,为④着色也只有4种方法。
∴ 共有着色方法6×5×4×4=480种
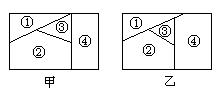 (2)与①的区别在于与④相邻的区域由两块变成了三块,同理,不同的着色方法数是n(n-1)(n-2)(n-3)
(2)与①的区别在于与④相邻的区域由两块变成了三块,同理,不同的着色方法数是n(n-1)(n-2)(n-3)
由n(n-1)(n-2)(n-3)=120
∴ (n2-3n)(n2-3n+2)-120=0
即(n2-3n)2+2(n2-3n)-12×10=0
∴ n2-3n-10=0
∴ n=5
例2、计算下列各题:
(1)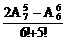
(2)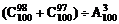
(3)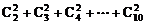
解:(1)原式=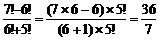
(2)原式=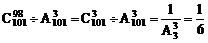
(3)原式=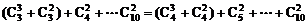
=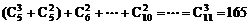
例3、按以下要求分配6本不同的书,各有几种分法?
(1)平均分给甲、乙、丙三人,每人2本;
(2)平均分成三份,每份2本;
(3)甲、乙、丙三人一人得1本,一人得2本,一人得3本;
(4)分成三份,一份1本,一份2本,一份3本;
(5)甲、乙、丙三人中,一人得4本,另二人每人得1本;
(6)分成三份,一份4本,另两份每份1本;
(7)甲得1本,乙得1本,丙得4本(均只要求列式)
解:(1)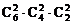 ;
;
(2)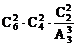
(3)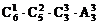
(4)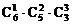
(5)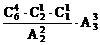
(6)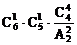
(7)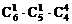
评注:有关排列组合混合题常常是先组合再排列。
例4、四面体的顶点和各棱中点共有10个点,在其中取4个不共面的点,不同的取法共有( )
A、150种 B、147种 C、144种 D、141种
解:从10个点中任取4个点有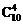 种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有
种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有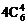 种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三种情况不合要求应减掉,所以不同的取法共有
种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三种情况不合要求应减掉,所以不同的取法共有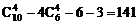 (种)
(种)
例5、求(4+2x+x2)(2-x)7的展开式中x5的系数。
解:(4+2x+x2)(2-x)7=(8-x3)(x-2)6
=(8-x3)[(x6-2C61x5+(-2)2C62x4+(-2)3C63x3+(-2)4C64x2+…]
∴ 含x5的项为-2×8×C61.x5-(-2)4C64x5=-336x5
∴ x5的系数为-336
例6、已知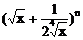 的展开式前三项中的x的系数成等差数列。
的展开式前三项中的x的系数成等差数列。
(1)求展开式里所有的x的有理项;
(2)求展开式里系数最大的项。
解:(1)∵
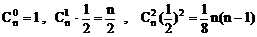
由题设可知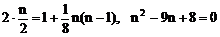
解得n=8或n=1(舍去)
当n=8时,通项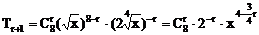
据题意, 必为整数,从而可知r必为4的倍数,而0≤r≤8
必为整数,从而可知r必为4的倍数,而0≤r≤8
∴ r=0,4,8,故x的有理项为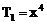 ,
,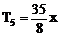 ,
,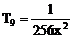
(3)设第r+1项的系数tr+1最大,显然tr+1>0,故有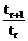 ≥1且
≥1且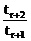 ≤1
≤1
∵ 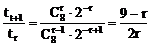
由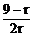 ≥1得r≤3
≥1得r≤3
又∵ 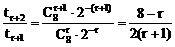
由 ≤1得:r≥2
≤1得:r≥2
∴ r=2或r=3所求项为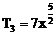 和
和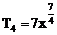
例7、设a>1,n∈N,且n≥2,求证: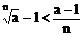
证明:设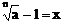 ,则(x+1)n=a
,则(x+1)n=a
欲证原不等式,即证nx<(x+1)n-1,其中x>0
∵ 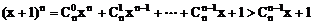
即(x+1)n>nx+1,原不等式成立。
评注:由于(a+b)n的展开式共有n+1项,故可通过对某些项的取舍来达到近似计算或证明不等式的目的。
例8、盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:
(1)取到的2只都是次品;
(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品。
解:从6只灯泡中有放回地任取两只,共有62=36种不同取法
(1)取到的2只都是次品情况为22=4种,因而所求概率为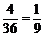
(2)由于取到的2只中正品、次品各一只有两种可能:第一次取到正品,第二次取到次品;及第一次取到次品,第二次取到正品。因而所求概率为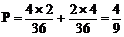
(3)由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件,因而所求概率为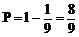
例9、甲、乙两人独立地破译1个密码,他们能译出的密码的概率分别为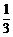 和
和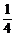 ,求:
,求:
(1)恰有1人译出的密码的概率;
(2)至多1人译出的密码的概率;
(3)若达到译出的密码的概率为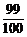 ,至少需要多少个乙这样的人。
,至少需要多少个乙这样的人。
解:记“甲译出密码”为事件A,“甲译不出密码”这事件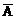 ;记“乙译出密码”为事件B,“乙译不出密码”为事件
;记“乙译出密码”为事件B,“乙译不出密码”为事件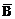 ;“两人都译出密码”为事件C,“两人都译不出密码”为事件D;“恰有1人译出密码”为事件E;“至多1人译出密码”为事件F。
;“两人都译出密码”为事件C,“两人都译不出密码”为事件D;“恰有1人译出密码”为事件E;“至多1人译出密码”为事件F。
(1)“恰有1人译出密码”是包括2种情况:一种是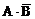 ,另一种是
,另一种是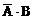 。这两种情况不能同时发生,是互斥的。
。这两种情况不能同时发生,是互斥的。
∴ 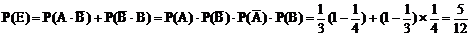
(2)“至多1人译出密码”包括两种情况:“2人都译不出密码”或“恰有1人译出密码”,即事件D+E,且事件D、E是互斥的
∴ 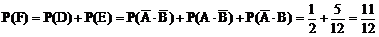
(3)n个乙这样的人都译不出密码的概率为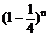 ,根据题意得:
,根据题意得: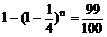
解得:n=16
例10、某数学家有两盒火柴,每盒都有n根火柴,每次用火柴时他在两盒中任取一盒并从中抽出一根,求他发现用完一盒时另一盒还有r根(1≤r≤n)的概率。
解析:由题意知:数学家共用了2n-r根火柴,其中n根取自一盒火柴,n-r根取自另一盒火柴。
由于数学家取火柴时,每次他在两盒中任取一盒并从中抽取一根,故他用完的那一盒取出火柴的概率是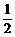 ,他不从此盒中取出一根火柴的概率也是
,他不从此盒中取出一根火柴的概率也是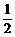 。
。
由于所取的2n-r根火柴,有n根取自用完的那一盒的概率为:
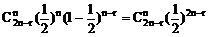
参考答案
(一) 选择题
1、B 2、B 3、B 4、A 5、D 6、D 7、A 8、C 9、C 10、C
11、A 12、B 13、B 14、C
(二) 填空题
15、211 16、-336
17、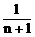 18、(1)1/3 (2)2/3 19、0.3671875
18、(1)1/3 (2)2/3 19、0.3671875
(三) 解答题
20、504 21、(1)90 (2)30 (3)90 22、4,-3
23、(1)0.41 (2)0.74
24、(1)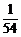 (2)
(2)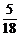 (3)
(3)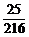 (4)
(4)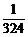
25、(1)0.56 (2)0.94 (3)0.38
26、(1)rn(2-rn) (2)rn(2-r)n (2)比(1)可靠