
网址:http://www.1010jiajiao.com/paper/timu/5146753.html[举报]
例1、 求下列极限
(1)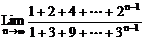 (2)
(2)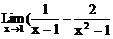 )
)
解题思路分析:
(1)因分子及分母的次数随n增大而增加,故不能利用运算性质。先求和化简。
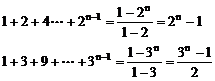
∴ 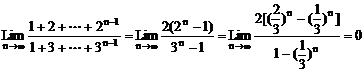
(2)当x→1时,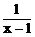 及
及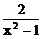 均无意义,应约去因式x-1
均无意义,应约去因式x-1
∵ 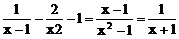
∴ 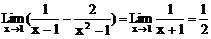
说明:函数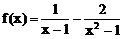 在x=1 无定义,但与
在x=1 无定义,但与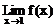 存在无关。一般地有下列结论:如果f(x)=x0处无定义,g(x)在x=x0处有定义并存在极限,且当x≠x0时,f(x)=g(x),则
存在无关。一般地有下列结论:如果f(x)=x0处无定义,g(x)在x=x0处有定义并存在极限,且当x≠x0时,f(x)=g(x),则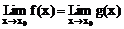 。
。
例2、设函数y=ax3+bx2+cx+d的图象与y轴交点为P,且曲线在P点处的切线方程为12x-y-4=0,若函数在x=2处取得极值0,试确定函数的解析式。
解题思路分析:
P(0,d)
∵ 曲线在点P处切线为12x-y-4=0
∴ x=0时,y=d
∴ d=-4
∵ y’=3ax2+2bx+c
∴ y’|x=0=c
又切线斜率k=12
∴ c=12
又函数在x=2处取得极值0
∴ 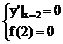
∴ 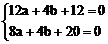
∴ 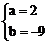
∴ 函数解析式y=2x3-9x2+12x-4
例3、偶函数f(x)=ax4+bx3+cx2+dx+e的图象过点P(0,1),且在x=1处的切线方程为y=x-2
(1)求y=f(x)的解析式;
(2)求y=f(x)的极大(小)值。
解题思路分析:
∵ f(x)是偶函数
∴ b=d=0
又图象过P(0,1)
∴ e=1
此时f(x)=ax4+cx2+1
∵ y’=4ax3+2cx
∴ y’|x=1=4a+2c=1 ①
又切点(1,-1)在曲线上
∴ a+c+1=-1 ②
由①②得: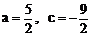
∴ f(x)=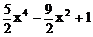
(2)f’(x)=10x3-9x=0
∴ x=0,x=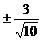
列表可得: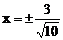 时,f(x)极小=
时,f(x)极小=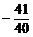
x=0时,f(x)极大=1
例4、曲线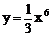 上哪一点的法线在y轴上截距最小?(法线是指过曲线上一点与以此点为切点的切线垂直的直线)
上哪一点的法线在y轴上截距最小?(法线是指过曲线上一点与以此点为切点的切线垂直的直线)
解题思路分析:
在曲线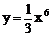 上任取一点(x0,y0),则过该点切线的斜率为k=2x05
上任取一点(x0,y0),则过该点切线的斜率为k=2x05
∴ 法线的斜率为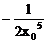
∴ 法线方程y-y0=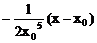
令x=0,使法线在y轴上的截距
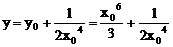
∴ 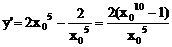
令y’=0,得x0=±1
当x0<-1时,y’<0,∴y单调递减
当-1<x0<0时,y’>0,∴y单调递增
当0<x0<1时,y’<0,∴y单调减小
当x0>1时,y’>0,则y单递增
∴ 当x0=±1时,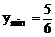 ,此时点(±1,
,此时点(±1,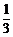 )
)
例5、研究函数f(x)=ax3+bx2-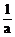 x+1的单调性(a≠0)
x+1的单调性(a≠0)
解题思路分析:
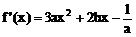
1、a>0时,由f’(x)>0得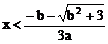 或
或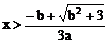
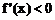 得
得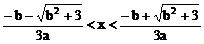
∴ f(x)在(-∞,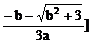 ,
,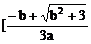 ,+∞)上单调递增;在
,+∞)上单调递增;在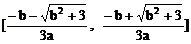 上单调递减。
上单调递减。
参考答案
(一)选择题
1、A 2、D 3、C 4、C 5、B 6、A 7、B 8、D 9、B 10、C 11、B 12、C
(二)填空题
13、a=b=1 14、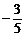 15、(-1,1)或(
15、(-1,1)或(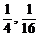 )
16、5与43
)
16、5与43
(三)解答题
17、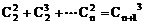 ……3分
……3分
∴ 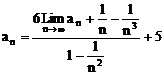 ……6分
……6分
∴ 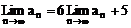 ……9分
……9分
∴ 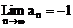 ……10分
……10分
18、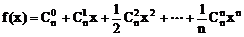
∴ 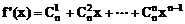 ……4分
……4分
∴ 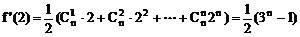 ……8分
……8分
∴  ……12分
……12分
19、设P(t,at2),则1斜率k1=2at
∴ 1:y-at2=2at(x-t) ……2分
2斜率k2=3bx2|x=1=3b
∴ 2:y-b=3b(x-1) ……4分
∵ 1与2于点M(2,2)
∴ 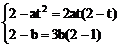
∴ 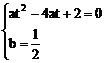 ①
①
又1⊥2
∴ k1k2=0
∴ 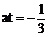 ②
……8分
②
……8分
由①②得t=10,a=-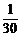
∴ P(10,-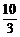 )
……10分
)
……10分
20、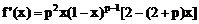 ……4分
……4分
令f’(x)=0得,x=0,x=1,x=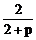 ……6分
……6分
在[0,1]上,f(0)=0,f(1)=0,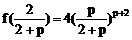 ……10分
……10分
∴ 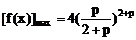 ……12分
……12分
21、设双曲线上任一点P(x0,y0)
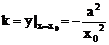 ……4分
……4分
∴ 切线方程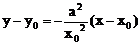 ……6分
……6分
令y=0,则x=2x0 ……8分
令x=0,则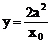 ……10分
……10分
∴ 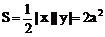 ……12分
……12分
22、y’=3x2+2px+q ……2分
令y’=0,设3x2+2px+q=0两根为x1,x2,x1<x2,列表:
|
x |
(-∞,x1) |
x1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
y’ |
+ |
0 |
- |
0 |
+ |
   y y |
|
极大值 |
|
极小值 |
|
∴ S与x轴相切于点(x1,0),点(x2,-4)在S上 ……6分
 x13+px12+qx1=0
①
x13+px12+qx1=0
①
∴ x23+px22+qx1=-4 ② ……8分
3x12+2px1+q=0 ③
3x22+2px2+q=0 ④
③×x1-①得:x1=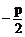
④×x2-②得:2x23+px22=4 ……10分
又x1+x2=-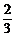 p
p
∴ x2= p,p=6
……12分
p,p=6
……12分
∴ x1=-3,x2=-1
∴ p=6,q=9 ……14分