
网址:http://www.1010jiajiao.com/paper/timu/5146755.html[举报]
(一) 选择题(每小题5分,共60分)
1、 等差数列中,若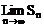 存在,则这样的数列
存在,则这样的数列
A、 有且仅有一个 B、有无数多个 C、有一个或无穷多个 D、不存在
2、 已知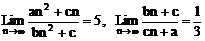 ,如果bc≠0,那么
,如果bc≠0,那么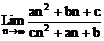 =
=
A、 15
B、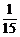 C、
C、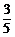 D、
D、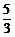
3、 若r为实常数,则集合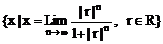
A、恰有一个元素 B、恰有两个元素 C、恰有三个元素 D、无数多个元素
4、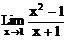 的值
的值
A、2 B、1 C、0 D、不存在
5、函数y=(x2-1)3+1在x=-1处
A、 有极大值 B、无极值 C、有极小值 D、无法确定极值情况
6、 f(x)=ax3+3x2+2,f’(-1)=4,则a=
A、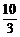 B、
B、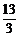 C、
C、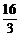 D、
D、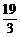
7、过抛物线y=x2上的点M(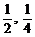 )的切线的倾斜角是
)的切线的倾斜角是
A、300 B、450 C、600 D、900
8、函数f(x)=x3-6bx+3b在(0,1)内有极小值,则实数b的取值范围是
A、 A、(0,1) B、(-∞,1)
C、(0,+∞) D、(0,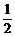 )
)
9、 函数y=x3-3x+3在[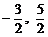 ]上的最小值是
]上的最小值是
A、 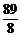 B、1 C、
B、1 C、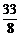 D、5
D、5
10、若f(x)=x3+ax2+bx+c,且f(0)=0为函数的极值,则
A、c≠0 B、当a>0时,f(0)为极大值
C、b=0 D、当a<0时,f(0)为极小值
11、已知函数y=2x3+ax2+36x-24在x=2处有极值,则该函数的一个递增区间是
A、(2,3) B、(3,+∞) C、(2,+∞) D、(-∞,3)
12、方程6x5-15x4+10x3+1=0的实数解的集合中
A、至少有2个元素 B、至少有3个元素 C、至多有1个元素 D、恰好有5个元素
参考答案
(一)选择题
1、A 2、D 3、C 4、C 5、B 6、A 7、B 8、D 9、B 10、C 11、B 12、C
(二)填空题
13、a=b=1 14、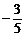 15、(-1,1)或(
15、(-1,1)或(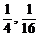 )
16、5与43
)
16、5与43
(三)解答题
17、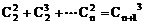 ……3分
……3分
∴ 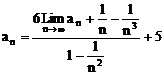 ……6分
……6分
∴ 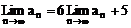 ……9分
……9分
∴ 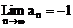 ……10分
……10分
18、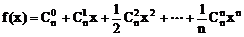
∴ 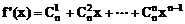 ……4分
……4分
∴ 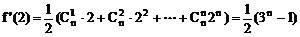 ……8分
……8分
∴  ……12分
……12分
19、设P(t,at2),则1斜率k1=2at
∴ 1:y-at2=2at(x-t) ……2分
2斜率k2=3bx2|x=1=3b
∴ 2:y-b=3b(x-1) ……4分
∵ 1与2于点M(2,2)
∴ 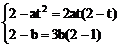
∴ 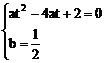 ①
①
又1⊥2
∴ k1k2=0
∴ 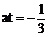 ②
……8分
②
……8分
由①②得t=10,a=-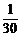
∴ P(10,-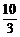 )
……10分
)
……10分
20、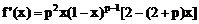 ……4分
……4分
令f’(x)=0得,x=0,x=1,x=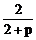 ……6分
……6分
在[0,1]上,f(0)=0,f(1)=0,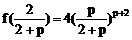 ……10分
……10分
∴ 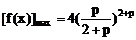 ……12分
……12分
21、设双曲线上任一点P(x0,y0)
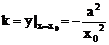 ……4分
……4分
∴ 切线方程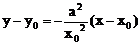 ……6分
……6分
令y=0,则x=2x0 ……8分
令x=0,则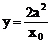 ……10分
……10分
∴ 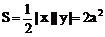 ……12分
……12分
22、y’=3x2+2px+q ……2分
令y’=0,设3x2+2px+q=0两根为x1,x2,x1<x2,列表:
|
x |
(-∞,x1) |
x1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
y’ |
+ |
0 |
- |
0 |
+ |
   y y |
|
极大值 |
|
极小值 |
|
∴ S与x轴相切于点(x1,0),点(x2,-4)在S上 ……6分
 x13+px12+qx1=0
①
x13+px12+qx1=0
①
∴ x23+px22+qx1=-4 ② ……8分
3x12+2px1+q=0 ③
3x22+2px2+q=0 ④
③×x1-①得:x1=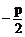
④×x2-②得:2x23+px22=4 ……10分
又x1+x2=-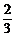 p
p
∴ x2= p,p=6
……12分
p,p=6
……12分
∴ x1=-3,x2=-1
∴ p=6,q=9 ……14分