网址:http://www.1010jiajiao.com/paper/timu/5146812.html[举报]
2、函数的通性
(1)奇偶性:函数定义域关于原点对称是判断函数奇偶性的必要条件,在利用定义判断时,应在化简解析式后进行,同时灵活运用定义域的变形,如 ,
,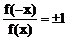 (f(x)≠0)。
(f(x)≠0)。
奇偶性的几何意义是两种特殊的图象对称。
函数的奇偶性是定义域上的普遍性质,定义式是定义域上的恒等式。
利用奇偶性的运算性质可以简化判断奇偶性的步骤。
(2)单调性:研究函数的单调性应结合函数单调区间,单调区间应是定义域的子集。
判断函数单调性的方法:①定义法,即比差法;②图象法;③单调性的运算性质(实质上是不等式性质);④复合函数单调性判断法则。
函数单调性是单调区间上普遍成立的性质,是单调区间上恒成立的不等式。
函数单调性是函数性质中最活跃的性质,它的运用主要体现在不等式方面,如比较大小,解抽象函数不等式等。
(3)周期性:周期性主要运用在三角函数及抽象函数中,是化归思想的重要手段。
求周期的重要方法:①定义法;②公式法;③图象法;④利用重要结论:若函数f(x)满足f(a-x)=f(a+x),f(b-x)=f(b+x),a≠b,则T=2|a-b|。
(4)反函数:函数是否是有反函数是函数概念的重要运用之一,在求反函数之前首先要判断函数是否具备反函数,函数f(x)的反函数f-1(x)的性质与f(x)性质紧密相连,如定义域、值域互换,具有相同的单调性等,把反函数f-1(x)的问题化归为函数f(x)的问题是处理反函数问题的重要思想。
设函数f(x)定义域为A,值域为C,则
f-1[f(x)]=x,x∈A
f[f-1(x)]=x,x∈C
(2) 求a的取值范围。
参考答案
(一) 选择题
1、 D 2、B 3、B 4、B 5、A 6、A
(二) 填空题
7、
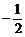 8、(0,1) 9、[
8、(0,1) 9、[ ] 10、f(bx)≤f(cx)
11、13
] 10、f(bx)≤f(cx)
11、13
12、
189 13、-1 14、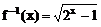 (x>0) 15、1
(x>0) 15、1
(三) 解答题
16、
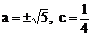 17.[-1,
17.[-1,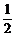 ]
]
18、(1)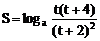 (t≥1)
(t≥1)
(2)在[1,+∞)上是减函数
(3)t=1时,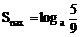
19、(1)a=1;
(2)当0<k≤2时,1-k<x<1;当k>2时,-1<x<1
20、