10. 求解析式
例15. 设函数存在反函数,与的图象关于直线对称,则函数
A. B.
C.
D.
分析:要求的解析式,实质上就是求图象上任一点的横、纵坐标之间的关系。
点关于直线的对称点适合,即。
又,
即,选B。
抽象函数的周期问题
--由一道高考题引出的几点思考
2001年高考数学(文科)第22题:设是定义在上的偶函数,其图象关于直线对称。对任意都有。
(I)设求;
(II)证明是周期函数。
解析:(I)解略。
(II)证明:依题设关于直线对称
故
又由是偶函数知
将上式中以代换,得
这表明是上的周期函数,且2是它的一个周期
是偶函数的实质是的图象关于直线对称
又的图象关于对称,可得是周期函数
且2是它的一个周期
由此进行一般化推广,我们得到
思考一:设是定义在上的偶函数,其图象关于直线对称,证明是周期函数,且是它的一个周期。
证明:关于直线对称
又由是偶函数知
将上式中以代换,得
是上的周期函数
且是它的一个周期
思考二:设是定义在上的函数,其图象关于直线和对称。证明是周期函数,且是它的一个周期。
证明:关于直线对称
将上式的以代换得
是上的周期函数
且是它的一个周期
若把这道高考题中的“偶函数”换成“奇函数”,还是不是周期函数?经过探索,我们得到
思考三:设是定义在上的奇函数,其图象关于直线对称。证明是周期函数,且4是它的一个周期。,
证明:关于对称
又由是奇函数知
将上式的以代换,得
是上的周期函数
且4是它的一个周期
是奇函数的实质是的图象关于原点(0,0)中心对称,又的图象关于直线对称,可得是周期函数,且4是它的一个周期。由此进行一般化推广,我们得到
思考四:设是定义在上的函数,其图象关于点中心对称,且其图象关于直线对称。证明是周期函数,且是它的一个周期。
证明:关于点对称
关于直线对称
将上式中的以代换,得
是上的周期函数
且是它的一个周期
由上我们发现,定义在上的函数,其图象若有两条对称轴或一个对称中心和一条对称轴,则是上的周期函数。进一步我们想到,定义在上的函数,其图象如果有两个对称中心,那么是否为周期函数呢?经过探索,我们得到
思考五:设是定义在上的函数,其图象关于点和对称。证明是周期函数,且是它的一个周期。
证明:关于对称
将上式中的以代换,得
是周期函数
且是它的一个周期
抽象函数解法例谈
抽象函数是指没有给出具体的函数解析式或图像,只给出一些函数符号及其满足的条件的函数,如函数的定义域,解析递推式,特定点的函数值,特定的运算性质等,它是高中函数部分的难点,也是大学高等数学函数部分的一个衔接点,由于抽象函数没有具体的解析表达式作为载体,因此理解研究起来比较困难.但由于此类试题即能考查函数的概念和性质,又能考查学生的思维能力,所以备受命题者的青睐,那么,怎样求解抽象函数问题呢,我们可以利用特殊模型法,函数性质法,特殊化方法,联想类比转化法,等多种方法从多角度,多层面去分析研究抽象函数问题,
一:函数性质法
函数的特征是通过其性质(如奇偶性,单调性周期性,特殊点等)反应出来的,抽象函数也是如此,只有充分挖掘和利用题设条件和隐含的性质,灵活进行等价转化,抽象函数问题才能转化,化难为易,常用的解题方法有:1,利用奇偶性整体思考;2,利用单调性等价转化;3,利用周期性回归已知4;利用对称性数形结合;5,借助特殊点,布列方程等.
二:特殊化方法
1在求解函数解析式或研究函数性质时,一般用代换的方法,将x换成-x或将x换成等
2在求函数值时,可用特殊值代入
3研究抽象函数的具体模型,用具体模型解选择题,填空题,或由具体模型函数对综合题,的解答提供思路和方法.
总之,抽象函数问题求解,用常规方法一般很难凑效,但我们如果能通过对题目的信息分析与研究,采用特殊的方法和手段求解,往往会收到事半功倍之功效,真有些山穷水复疑无路,柳暗花明又一村的快感.

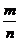 )的值
)的值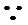 f(0) =f(0+0)=f(0) .f(0)=f2(0)
f(0) =f(0+0)=f(0) .f(0)=f2(0)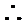 f(0) =0或1.若f(0)=0则f(4)=16=f(0+4)=f(0) .f(4)=0.(矛盾)
f(0) =0或1.若f(0)=0则f(4)=16=f(0+4)=f(0) .f(4)=0.(矛盾) f(1)=1
f(1)=1 f(4)=f(2) .f(2)=f(1) .f(1) .f(1)
.f(1)=16
f(4)=f(2) .f(2)=f(1) .f(1) .f(1)
.f(1)=16 )≥0
)≥0 f(1)=2.仿此可证得f(a)≥0.即y=f(x)是非负函数.
f(1)=2.仿此可证得f(a)≥0.即y=f(x)是非负函数. f(-a)=
f(-a)=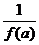
 n∈N*时f(n)=fn(1)=2n,f(-n)=2-n
n∈N*时f(n)=fn(1)=2n,f(-n)=2-n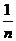 +
+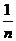 +…+
+…+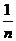 )=fn(
)=fn(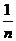 )=2
)=2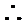 f(
f(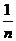 )=
)= 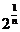
 f(
f(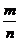 )=[f(
)=[f( )]m=
)]m=