3. (北京卷)设f(x)是定义在[0,
1]上的函数,若存在x*∈(0,1),使得f(x)在[0, x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0, 1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,l]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x*,1)为含峰区间;
(II)对给定的r(0<r<0.5),证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(I)所确定的含峰区间的长度不大于 0.5+r;
(III)选取x1,x2∈(0, 1),x1<x2,由(I)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0.34.(区间长度等于区间的右端点与左端点之差)
解:(I)证明:设x*为f(x) 的峰点,则由单峰函数定义可知,f(x)在[0, x*]上单调递增,在[x*,
1]上单调递减.
当f(x1)≥f(x2)时,假设x*(0, x2),则x1<x2<x*,从而f(x*)≥f(x2)>f(x1),
这与f(x1)≥f(x2)矛盾,所以x*∈(0, x2),即(0, x2)是含峰区间.
当f(x1)≤f(x2)时,假设x*( x2, 1),则x*<≤x1<x2,从而f(x*)≥f(x1)>f(x2),
这与f(x1)≤f(x2)矛盾,所以x*∈(x1, 1),即(x1, 1)是含峰区间.
(II)证明:由(I)的结论可知:
当f(x1)≥f(x2)时,含峰区间的长度为l1=x2;
当f(x1)≤f(x2)时,含峰区间的长度为l2=1-x1;
对于上述两种情况,由题意得
①
由①得 1+x2-x1≤1+2r,即x1-x1≤2r.
又因为x2-x1≥2r,所以x2-x1=2r, ②
将②代入①得
x1≤0.5-r, x2≥0.5-r,
③
由①和③解得 x1=0.5-r, x2=0.5+r.
所以这时含峰区间的长度l1=l1=0.5+r,即存在x1,x2使得所确定的含峰区间的长度不大于0.5+r.
(III)解:对先选择的x1;x2,x1<x2,由(II)可知
x1+x2=l,
④
在第一次确定的含峰区间为(0, x2)的情况下,x3的取值应满足
x3+x1=x2,
⑤
由④与⑤可得,
当x1>x3时,含峰区间的长度为x1.
由条件x1-x3≥0.02,得x1-(1-2x1)≥0.02,从而x1≥0.34.
因此,为了将含峰区间的长度缩短到0.34,只要取
x1=0.34,x2=0.66,x3=0.32.
4(上海)已知函数f(x)=kx+b的图象与x、y轴分别相交于点A、B,( 、分别是与x、y轴正半轴同方向的单位向量), 函数g(x)=x2-x-6.
(1)求k、b的值;
(2)当x满足f(x)> g(x)时,求函数的最小值.
[解](1)由已知得A(,0),B(0,b),则={,b},于是=2,b=2. ∴k=1,b=2.
(2)由f(x)> g(x),得x+2>x2-x-6,即(x+2)(x-4)<0, 得-2<x<4,
==x+2+-5
由于x+2>0,则≥-3,其中等号当且仅当x+2=1,即x=-1时成立
∴的最小值是-3.
5,(上海)(本题满分18分)本题共有3个小题,第1小题满分4分, 第2小题满分8分, 第3小题满分6分.
对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
f(x).g(x) 当x∈Df且x∈Dg
规定: 函数h(x)=
f(x) 当x∈Df且xDg
g(x)
当xDf且x∈Dg
(1) 若函数f(x)=-2x+3,x≥1; g(x)=x-2,x∈R,写出函数h(x)的解析式;
(2) 求问题(1)中函数h(x)的最大值;
(3) 若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos2x,并予以证明.

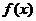 在
在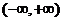 上满足
上满足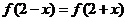 ,
,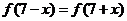 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有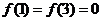 .
.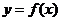 的奇偶性;
的奇偶性;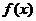 =0在闭区间[-2005,2005]上的根的个数,并证明你的结论.
=0在闭区间[-2005,2005]上的根的个数,并证明你的结论.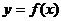 的对称轴为
的对称轴为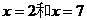 ,
,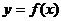 不是奇函数,
不是奇函数,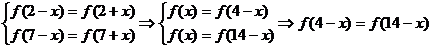
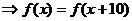 ,从而知函数
,从而知函数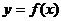 的周期为
的周期为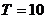
 ,故函数
,故函数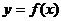 是非奇非偶函数;
是非奇非偶函数;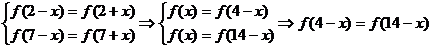
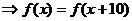
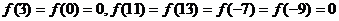
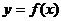 在[0,2005]上有402个解,在[-2005.0]上有400个解,所以函数
在[0,2005]上有402个解,在[-2005.0]上有400个解,所以函数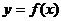 在[-2005,2005]上有802个解.
在[-2005,2005]上有802个解.