网址：http://www.1010jiajiao.com/paper/timu/5149432.html[举报]
2、口袋里装有大小相同的4个红球和8个白球，甲、乙两人依规则从袋中有放回摸球，每次摸出一个球，规则如下：若一方摸出一个红球，则此人继续下一次摸球；若一方摸出一个白球，则由对方接替下一次摸球，且每次摸球彼此相互独立，并由甲进行第一次摸球.
(I)求在前三次摸球中，甲摸得红球的次数ξ的数学期望；
(II)设第n次由甲摸球的概率为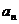
，试建立
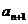与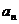的递推关系，并求数列{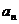}的通项公式.
解：(I)记“甲摸球一次摸出红球”为事件A，“乙摸球一次摸出红球”为事件B，则
，且A、B相互独立.………………(2分)
据题意，ξ的可能取值为0，1，2，3，其中
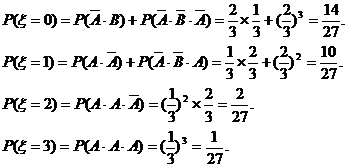
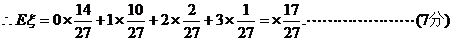
(II)据摸球规则可知，第n次由甲摸球包括如下两个事件：
①第n－1次由甲摸球，且摸出红球，其发生的概率为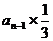
；
②第n－1次由乙摸球，且摸出白球，其发生的概率为
.
∵上述两个事件互斥，
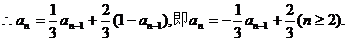……………………(10分)
由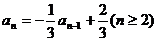
，
∵甲进行第一次摸球，
，即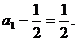
………………………………(12分)
∴数列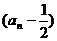
是首项为
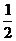，公比为－
的等比数列，
.
故
.……………………………………………………………(14分)