
网址:http://www.1010jiajiao.com/paper/timu/5150300.html[举报]
16.设 ,若
,若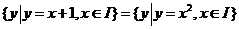 ,则
,则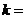 .
.
参考答案
|
11)若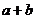 不是偶数,则
不是偶数,则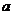 ,
,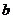 不都是偶数. 12)840 13)1 14)6
15)
不都是偶数. 12)840 13)1 14)6
15)
16)0或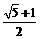 17)
17)
18.解: (1)设公比为 ,由题意知,
,由题意知,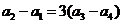 ,
,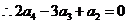 ,
,
即 ,即
,即 ,
, ,
,
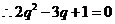 .
.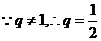 ,
, .
.
(2) 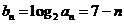 ,
,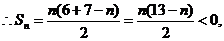
即 时,
时, 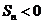 .
. 从第14项起,
从第14项起, 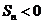 .
.
19.解: (1)由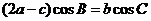 得
得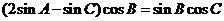 ,
,
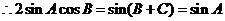 ,
, ,
,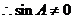 ,
,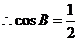 ,
,
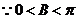 ,
,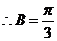 .
.
(2) 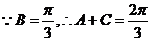 ,
,



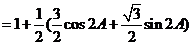

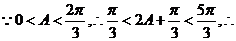 当
当 ,
,
即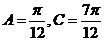 时,
时, 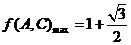 .
.
20.(1)证明:设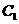 在底面的射影为
在底面的射影为 ,
,

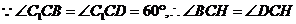 ,即
,即 点在对角线
点在对角线 上.
上. ,
,
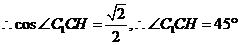 ,
,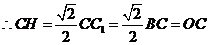 ,
,
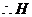 点即为
点即为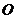 点,即
点,即 平面
平面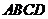 .
.
(2)分别以 为
为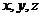 轴建立空间直角坐标系
轴建立空间直角坐标系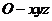 ,设边长为
,设边长为 ,
,
则 ,
,
而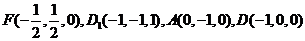 ,
,
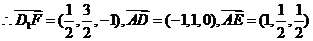 ,设平面
,设平面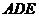 的法向量为
的法向量为
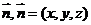 ,则
,则
 可取为
可取为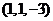 ,设
,设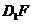 与平面
与平面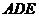 所成角为
所成角为 ,
,
则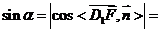
 ,
,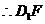 与平面
与平面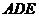 所成角为
所成角为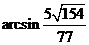 .
.
21. 解: (1)设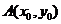 ,则
,则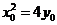 ,则圆
,则圆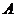 的半径
的半径 ,则圆
,则圆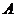 的方程为
的方程为
 ,令
,令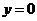 ,并将
,并将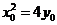 代入得
代入得 ,解得
,解得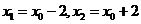 ,
,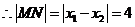 为定值.
为定值.
(2)不妨设 ,由
,由
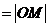
 知,
知,
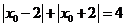 ,
, 到抛物线准线
到抛物线准线 的距离
的距离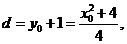
又圆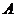 的半径
的半径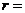
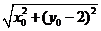 =
= ,
,

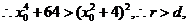
即圆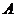 与抛物线的准线总相交.
与抛物线的准线总相交.
22. 解:(1)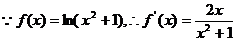 ,由
,由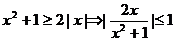
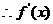 的值域为[-1,1]
的值域为[-1,1]
(2)∵m为方程f(x)=x的根,∴f(m)-m=0.
令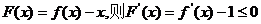
∴F(x)为单调减函数,∴当x>m时,F(x)<F(m),即当x>m时,
∴当x>m时,f(x)<x.
(3)令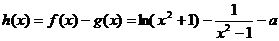 ,
,
 ,
,
当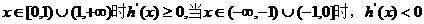
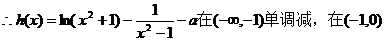 单调递减;
单调递减;
在(0,1)和(1,+∞)单调增
∴当x∈(-1,1)时,
x→-1-时,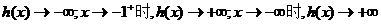
由h(x)为偶函数得,x→-1-时,h(x)→∞,x→1+,时,f(x)→-∞,
x→+∞时,h(x)→+∞

(若考虑到h(x)是偶函数,题意等价转化为h(x)在x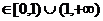 上有2实根的问题,因而只需研究h(x)在
上有2实根的问题,因而只需研究h(x)在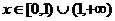 上单调性与h(0)的值以及h(x)在x→1+,x→1-,x→+∞的极限值,则可参照赋分,若仅从图象直观说明,则酌情扣分)
上单调性与h(0)的值以及h(x)在x→1+,x→1-,x→+∞的极限值,则可参照赋分,若仅从图象直观说明,则酌情扣分)