网址:http://www.1010jiajiao.com/paper/timu/5150398.html[举报]
17、(本题满分12分,第1小题8分,第2小题4分)
已知函数
(1)
求函数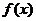 的周期;
的周期;
(2)
函数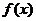 的图象可由函数
的图象可由函数 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
参考答案
一、选择题(本大题共6小题,每小题5 分,共30分)
ABDADB
二、填空题(本大题共10小题,每小题5分,共50分,把答案填在题中横线上)
7、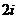 ;8、
;8、 ;9、75;10、
;9、75;10、 ;11、
;11、 ;12、11;13、
;12、11;13、 ;
;
14、 ;15、
;15、 ;16、
;16、
三、解答题
17、解:(1)

所以 函数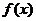 的周期是
的周期是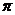 ………………………………………………8分
………………………………………………8分
(2)将函数 的图象向左平移
的图象向左平移 个单位,再将所得图象上每一点的横坐标变为原来的
个单位,再将所得图象上每一点的横坐标变为原来的 倍(纵坐标不变式),得函数
倍(纵坐标不变式),得函数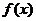 的图象………………………12分。
的图象………………………12分。
18、解:设地面矩形在门正下方的一边长为 ,则另一边的长为
,则另一边的长为 ………2分
………2分
设总造价为 元,则
元,则
 …………………………………………………………………………………7分
…………………………………………………………………………………7分
因为 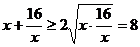
当且仅当 (
( 即
即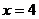 时 取“=”…………………………9分
时 取“=”…………………………9分
所以,当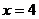 时
时 有最小的值
有最小的值 此时
此时 ……………………11分
……………………11分
答:当储藏室地面矩形在门正下方的一边长为 ,另一边的长为
,另一边的长为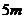 时,能使总造价最低造价为17000元。……………………………………………………12分。
时,能使总造价最低造价为17000元。……………………………………………………12分。
19、解:(1)
 ,
,

 …………3分
…………3分
(2)当点 为
为 的中点时,
的中点时, 。…………4分
。…………4分
理由如下: 点
点 分别为
分别为 、PD的中点,
、PD的中点,

 。
。

 ,
,
 …………………………………………7分
…………………………………………7分
(3)
 ,
,

 ,
,
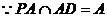 ,
,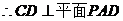

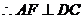 …………………………………10分
…………………………………10分
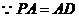 ,点
,点 是
是 的中点
的中点 
又
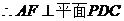

 ………………………………12分
………………………………12分
20、解:(1)由 及
及 ,得:
,得:
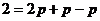
 ……………………………………………………4分
……………………………………………………4分
(2)由 ①
①
得 ②
②
由②-①,得 
即: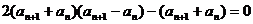

由于数列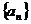 各项均为正数,
各项均为正数,
 即
即  ……………………………………6分
……………………………………6分
 数列
数列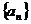 是首项为
是首项为 ,公差为
,公差为 的等差数列,
的等差数列,
 数列
数列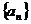 的通项公式是
的通项公式是  ……………9分
……………9分
(3)由 ,得:
,得:
 ……………………………………………………11分
……………………………………………………11分
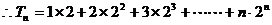



21、解:(1)
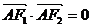 ,
,

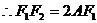 ,
, …………………………3分
…………………………3分
 ,
,
 ………………………………………5分
………………………………………5分
(2) ,
, 。
。
①若 垂直于
垂直于 轴,则
轴,则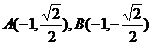 ,
,
 ,
,

②若 与
与 轴不垂直,设直线
轴不垂直,设直线 的斜率为
的斜率为 ,则直线
,则直线 的方程为
的方程为

由 得
得 
 ,
, 方程有两个不等的实数根。
方程有两个不等的实数根。
设 ,
, .
.
 ,
,  ………………………………9分
………………………………9分
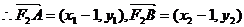



= ……………………………………12分
……………………………………12分
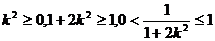 …………………………………13分
…………………………………13分
 ,所以当直线
,所以当直线 垂于
垂于 轴时,
轴时, 取得最大值
取得最大值
当直线 与
与 轴重合时,
轴重合时, 取得最小值
取得最小值 …………………………14分
…………………………14分
22、解:(1)由题意
 ………………………………………………2分
………………………………………………2分
 当
当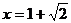 时,
时,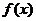 取得极值,
取得极值,
 所以
所以


 即
即 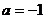 …………………………5分
…………………………5分
此时当 时,
时, ,当
,当 时,
时,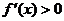 ,
,
 是函数
是函数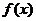 的最小值。………………………………………8分
的最小值。………………………………………8分
(2)设 ,则
,则  ,
,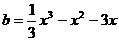 ……10分
……10分
设 ,
,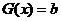
 ,令
,令 解得
解得 或
或
列表如下:
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
__ |
0 |
+ |
|
 |
 |
 |
 |
 |
 |
 |
 |
 函数
函数 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数。
上是减函数。
当 时,
时, 有极大值
有极大值 ;当
;当 时,
时, 有极小值
有极小值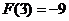 ……14分
……14分
 函数
函数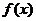 与
与 的图象有两个公共点,
的图象有两个公共点, 函数
函数 与
与 的图象有两个公共点
的图象有两个公共点
 或
或