
网址:http://www.1010jiajiao.com/paper/timu/5150498.html[举报]
22、已知椭圆 与射线y=
与射线y=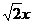 (x
(x 交于点A,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。
交于点A,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。
(1)求证:直线BC的斜率为定值,并求这个定值。
(2)求三角形ABC的面积最大值。
解几单元试卷参考答案
一、选择题:
1、A 2、C 3、B 4、D 5、B 6、A
7、C 8、C 9、B 10、D 11、C 12、B
二、填空题:
13、 14、椭圆
14、椭圆
15、 16、
16、
三、 解答题:
解答题:
17:解:由
得两直线交点的坐标 ,
,
又由题意知S1:S2=2:3或3:2
所以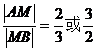 由A (-4,0),B(6,0) 根据定比分点公式得
由A (-4,0),B(6,0) 根据定比分点公式得
M(0,0)或M(2,0),所以所求直线的方程就是经过P和M两点的直线方程
所以所求直线的一般式方程是
18: 解:由题意直线 与圆
与圆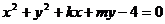 交于
交于 两点,且
两点,且 关于直线
关于直线 对称,则
对称,则 与
与 两直线垂直,可求出
两直线垂直,可求出 ,又不等式组所表示的平面区域应用线线规划去求,易得面积为
,又不等式组所表示的平面区域应用线线规划去求,易得面积为
19、解:设 ,则直线
,则直线 方程为:
方程为: ,由
,由
得 ,当且仅当
,当且仅当
当入射点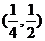 ,反射点
,反射点 时
时 最短。
最短。
20、解:由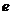 =
= 得
得 ,所以椭圆方程设为
,所以椭圆方程设为
设直线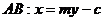 ,由
,由 得:
得:
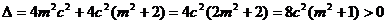
设 ,则
,则 是方程的两个根
是方程的两个根
由韦达定理得 所以
所以


=
当且仅当 时,即
时,即 轴时取等号
轴时取等号 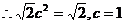
所以,所求椭圆方程为
21、解:已知焦点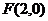 ,准线
,准线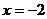 ,设椭圆半焦距为
,设椭圆半焦距为 ,半短轴长为
,半短轴长为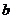 ,
,
椭圆中心 ,又
,又 即
即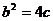

①当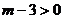 即
即 时,此时
时,此时


②当 时,即
时,即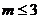 ,此时由于
,此时由于 ,所以
,所以 无最小值。
无最小值。
所以,所求 此时椭圆方程为
此时椭圆方程为 。
。
22、解:(!)由题意得 ,设
,设 的斜率为
的斜率为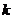 ,则
,则 的斜率为-
的斜率为-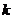
所以 代入得
代入得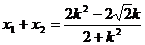 ,又
,又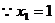
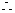
 同理
同理
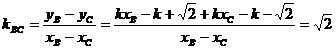 为定值
为定值
(1)设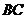 方程为
方程为
 得
得
 得
得
 到
到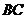 的距离为
的距离为
所以
当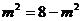 时,即
时,即 时“=”成立,此时
时“=”成立,此时 成立。
成立。