
网址:http://www.1010jiajiao.com/paper/timu/5150657.html[举报]
4.复数 (m∈R,i为虚数单位)在复平面上对应的点不可能位于 ( )
(m∈R,i为虚数单位)在复平面上对应的点不可能位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
高中毕业班质量检查数学(理科)试题参考答案
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则。
二、对计算题,当考生的解答在某一步出现错误时,如果后断部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答给分数的一半;如果后继部分的解答在较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数。选择题和填空题不给中间分。
一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分。
|
7.B 8.C 9.C 10.D 11.C 12.C
二、填空题:本题考查基础知识和基本运算,每小题4分,满分16分。
13.8
14.2
15.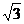 16.(1,1),(2,2),(3,4),(4,8)
16.(1,1),(2,2),(3,4),(4,8)
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤,在答题卡上相应题目的答题区域内作答。
17.本小题主要考查向量的数量积、三角形面积、有关三角函数的基本知识,以及基本的计算能力,满分12分。
解:(1)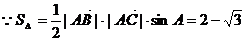 , ①…………………2分
, ①…………………2分
又 ,
,
 ②……………… 4分
②……………… 4分
由①、②得 ……………………………………………………… 6分
……………………………………………………… 6分
(2)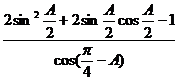
 ……………………………………………………………… 8分
……………………………………………………………… 8分
 …………………………………………………………………… 10分
…………………………………………………………………… 10分

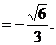 ……………………………………………………………………………12分
……………………………………………………………………………12分
18.本小题考查离散型随机变量分布列和数学期望等概念,考查运用概率、统计知识分析解决实际问题的能力,满分12分。
解:(1)设考生甲、乙正确完成实验操作的题数分别为ξ、η,
则ξ取值分别为1,2,3;η取值分别为0,1,2,3 ………………………………2分
 ,
,
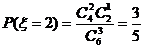 ,
,
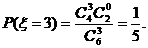
∴考生甲正确完成题数的概率分布列为:
|
ξ |
1 |
2 |
3 |
|
P |
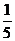 |
 |
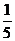 |
………………………………………………4分
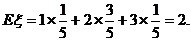 ………………………………………………5分
………………………………………………5分
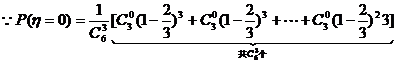
 ,
,
同理:
方法一:∴考生乙正确完成题数的概率分布列为:
|
η |
0 |
1 |
2 |
3 |
|
P |
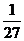 |
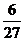 |
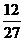 |
 |
……………………………………………………………………………7分
 …………………………………… 8分
…………………………………… 8分
方法二:同方法一得考乙正确完成题数的概率分布列为:
|
η |
0 |
1 |
2 |
3 |
|
P |
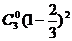 |
 |
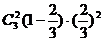 |
 |
………………………………………………………………………7分
∴考生乙做对题数η服从二项分布,
因此, …………………………………………………………8分
…………………………………………………………8分
(2)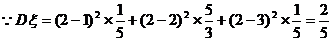 ,
,
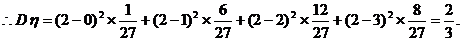
(或 )
)

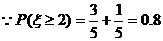 ,
,
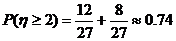 ,
,

从做对题数的数学期望考察,两人水平相当;从做对题数的方差考察,甲较稳定;从至少完成2题的概率考察,甲获得通过的可能性大,因此可以判断甲的实验操作能力较强。
………………………………………………12分
(第(2)问4分的安排说明:①依据期望说明两人水平相当,得1分;②计算方差、依据方差说明甲稳定性好,得1分;③依据通过的概率说明甲通过的可能性大,得1分;④给出结论:甲的实验操作能力较强,再给1分,如果只回答①、②、④,也给4分)
19.本小题主要考查面关系,异面直线所成的角以及点到平面距离等基础知识,考查空间想象能力,逻辑思维能力和运算能力。满分12分。
|
(1)证明:取AB中点H,连结GH,HE,
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH∥AD∥EF,
∴E,F,G,H四点共面. ……………………1分
又H为AB中点,
∴EH∥PB. ……………………………………2分
又EH 面EFG,PB
面EFG,PB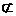 平面EFG,
平面EFG,
∴PB∥平面EFG. ………………………………3分
(2)解:取BC的中点M,连结GM、AM、EM,则GM//BD,
|
所成的角.………………4分
在Rt△MAE中, 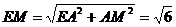 ,
,
同理 ,…………………………5分
,…………………………5分
又GM= ,
,
∴在△MGE中,
 ………………6分
………………6分
故异面直线EG与BD所成的角为arccos ,………………………………7分
,………………………………7分
(3)假设在线段CD上存在一点Q满足题设条件,
|
∵ABCD是正方形,△PAD是直角三角形,且PA=AD=2,
∴AD⊥AB,AD⊥PA.
又AB∩PA=A,
∴AD⊥平面PAB. ……………………………………8分
又∵E,F分别是PA,PD中点,
∴EF∥AD,∴EF⊥平面PAB.
又EF 面EFQ,
面EFQ,
∴面EFQ⊥面PAB. …………………………………9分
过A作AT⊥ER于T,则AT⊥平面EFQ,
∴AT就是点A到平面EFQ的距离. ……………………………………………10分
设 ,
,
在 ,
…………………………11分
,
…………………………11分
解得
故存在点Q,当CQ= 时,点A到平面EFQ的距离为0.8. ……………………… 12分
时,点A到平面EFQ的距离为0.8. ……………………… 12分
解法二:建立如图所示的空间直角坐标系A-xyz,
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
|
(1)证明: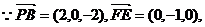
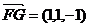 …………………………1分
…………………………1分
设 ,
,
即 ,
,
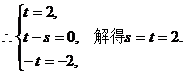
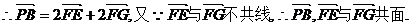 ……………2分
……………2分
 ,
,
∴PB∥平面EFG. …………………………………………………………………… 3分
(2)解:∵ ,…………………………………………4分
,…………………………………………4分
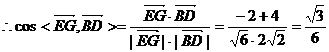 ,……………………… 6分
,……………………… 6分
故异面直线EG与BD所成的角为arcos .…………………………………… 7分
.…………………………………… 7分
(3)解:假设线段CD上存在一点Q满足题设条件,
令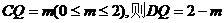
∴点Q的坐标为(2-m,2,0),
 ………………………………………………………………8分
………………………………………………………………8分
而 ,
,
设平面EFQ的法向量为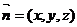 ,则
,则
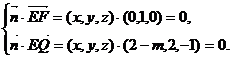

令 ,
……………………………………………………9分
,
……………………………………………………9分
又 ,
,
∴点A到平面EFQ的距离 ,……………10分
,……………10分
即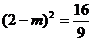 ,
,
 不合题意,舍去.
不合题意,舍去.
故存在点Q,当CQ= 时,点A到平面EFQ的距离为0.8. ……………………12分
时,点A到平面EFQ的距离为0.8. ……………………12分
20.本小题主要考查等差数列、递推规律的基本知识,以及运用这些知识解决实际问题的能力,满分12分。
解:(1)由题意规律,编号为2的同学看到的像是(6,8);
编号为3的同学看以的像是(8,11) ……………………………………………4分
(2)设编号为n的同学看到的像是(bn,an),
由 ,
,
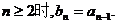 ……………………………………………………………… 5分
……………………………………………………………… 5分
由题意 ,
, 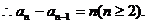 ………………………………6分
………………………………6分
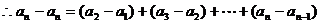

 …………………………………………………… 9分
…………………………………………………… 9分



 ……………………………………………………11分
……………………………………………………11分
经检验n =1时,上式也成立
∴编号为n的同学看到的像是 …………………… 12分
…………………… 12分
21.本小题主要考查双曲线的定义与方程,考查直线与圆锥曲线的位置关系、两直线垂直等基础知识,考查解析几何的基本思想和综合解题能力,满分12分。
解:(1)由 知,点P的轨迹E是以F1、F2为焦点的双曲线右支,由
知,点P的轨迹E是以F1、F2为焦点的双曲线右支,由 ,故轨迹E的方程为
,故轨迹E的方程为 …………3分
…………3分
(2)当直线l的斜率存在时,设直线方程为 ,与双曲线方程联立消y得
,与双曲线方程联立消y得 ,
,

解得k2 >3 ………………………………………………………………………………5分
(i)
|

 ,
,
故得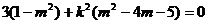 对任意的
对任意的
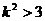 恒成立,
恒成立,
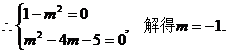
∴当m =-1时,MP⊥MQ.
当直线l的斜率不存在时,由 知结论也成立,
知结论也成立,
综上,当m =-1时,MP⊥MQ. ……………………………………………………8分
(ii) 是双曲线的右准线,……………………………9分
是双曲线的右准线,……………………………9分
由双曲线定义得: ,
,
方法一:
 ………10分
………10分
 ,…………………………………………11分
,…………………………………………11分
注意到直线的斜率不存在时,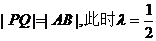 ,
,
综上,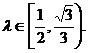 ………………………………………………………………12分
………………………………………………………………12分
方法二:设直线PQ的倾斜角为θ,由于直线PQ与双曲线右支有二个交点,
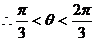 ,过Q作QC⊥PA,垂足为C,则
,过Q作QC⊥PA,垂足为C,则
|
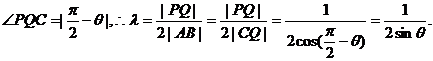 …………10分
…………10分
由
故: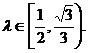 ………………12分
………………12分
22.本小题主要考察函数、导数、方程、不等式
等知识以及综合分析能力,满分14分。
解: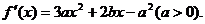 ………1分
………1分
(1) 是函数f(x)的两个极值点,
是函数f(x)的两个极值点,
 ………………………………………………………………2分
………………………………………………………………2分
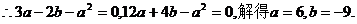 ………………………3分
………………………3分
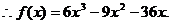 …………………………………………………………4分
…………………………………………………………4分
(2)∵x1、x2是 f(x)是两个极值点,
∴x1、x2是方程 的两根.
的两根.
∵△= 4b2 + 12a3, ∴△>0对一切a > 0, 恒成立.
恒成立.

 ……………………6分
……………………6分
由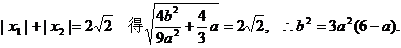 ………………7分
………………7分
 ………………………………………… 8分
………………………………………… 8分
令
 在(0,4)内是增函数;
在(0,4)内是增函数;
 ∴h (a)在(4,6)内是减函数.
∴h (a)在(4,6)内是减函数.
∴a = 4时,h(a)有极大值为96, 上的最大值是96,
上的最大值是96,
∴b的最大值是 …………………………………………………………………10分
…………………………………………………………………10分
(3)证法一:∵x1、x2是方程 的两根,
的两根,
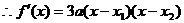 ,…………………………………………………… 11分
,…………………………………………………… 11分
 ………… 12分
………… 12分

 ……………………………………14分
……………………………………14分
证法二:∵x1、x2是方程 的两根,
的两根,
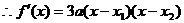 .…………………………………………………… 11分
.…………………………………………………… 11分


∵x1 < x < x2,
 ………………………………………………… 12分
………………………………………………… 12分

 ……………………………………………14分
……………………………………………14分