
网址:http://www.1010jiajiao.com/paper/timu/5151736.html[举报]
17.(本题满分12分)
已知复数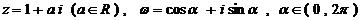 ,若
,若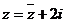 ,且
,且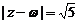 ,求角
,求角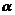 的值.
的值.
[解]
数学试卷(文史类)参考答案与评分标准(理科) 2007/4
一、填空题
1.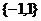 2.
2.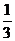 3.
3. 4.80
5.4
6.5
7.
4.80
5.4
6.5
7.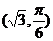
8.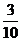 9.2
10.
9.2
10.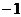 11.③④
11.③④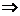 ①②或①④
①②或①④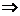 ②③
②③
12.已知空间四边形一组对边的平方和等于另一组对边的平方和,则空间四边形余下的一组对边(对角线)互相垂直.
二、选择题
13.B 14.A 15.D 16.A
三、解答题
17.解:由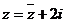 得:
得: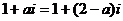 ,所以
,所以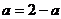 ,
,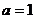 ---------------4分
---------------4分
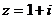 ,
,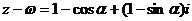 -------------------------------------------5分
-------------------------------------------5分
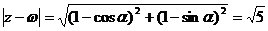 ----------------------------------------------7分
----------------------------------------------7分
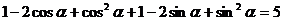 ,
,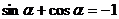 --------------8分
--------------8分
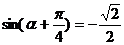 ------------------10分
------------------10分 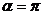 或
或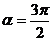 --------------------12分
--------------------12分
18.解:(1)由已知: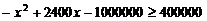 ,即
,即
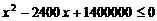 ,解得
,解得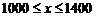 ---------------------------------4分
---------------------------------4分
又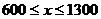 ,所以景区游客人数的范围是1000至1300人 -------------5分
,所以景区游客人数的范围是1000至1300人 -------------5分
(2)设游客的人均消费额为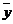 ,则
,则
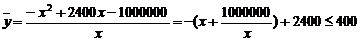 ----------------------9分
----------------------9分
当且仅当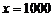 时等号成立.
----------------------------------------------------12分
时等号成立.
----------------------------------------------------12分
答:当景区游客的人数为 时,游客的人均消费最高,最高消费额为
时,游客的人均消费最高,最高消费额为 元.
元.
19.解:(1)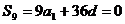 ,得:
,得: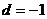 ,
,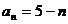 -----------------------------2分
-----------------------------2分
由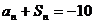 ,
,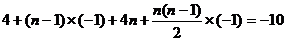
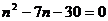 ,得到
,得到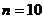 -------------------------------------------------6分
-------------------------------------------------6分
(2)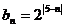 ,
,
若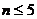 ,则
,则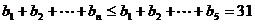 ,不合题意-----------------9分
,不合题意-----------------9分
故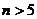 ,
,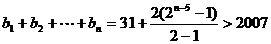 -------------------------------11分
-------------------------------11分
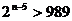 ,所以
,所以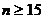 ,使不等式成立的最小正整数
,使不等式成立的最小正整数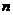 的值为15.-----------14分
的值为15.-----------14分
20.解:(1)方法一:如图,分别以CA、DB为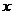 、
、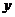 轴建立空间直角坐标系.
轴建立空间直角坐标系.
因为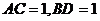 ,所以
,所以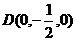 ,
,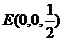 ,
,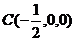
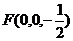
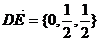 ,
,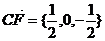 ---------------4分
---------------4分 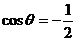 -----------------6分
-----------------6分
因为异面直线所成角为锐角,故异面直线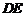 与
与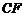 所成的角为
所成的角为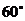 ----------------7分
----------------7分
方法二:见文科答案与评分标准.
 (2)正子体体积不是定值.-------------8分
(2)正子体体积不是定值.-------------8分
设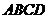 与正方体的截面四边形为
与正方体的截面四边形为
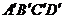 , 设
, 设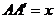
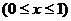
则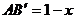 ----------------------------9分
----------------------------9分
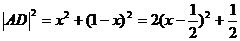
故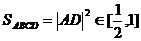 ----------------------------------------------------------------------12分
----------------------------------------------------------------------12分
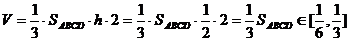 -----------------------------14分
-----------------------------14分
21.解:(1)∵对任意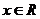 ,
,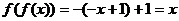 ,∴
,∴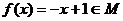 --2分
--2分
∵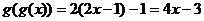 不恒等于
不恒等于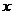 ,∴
,∴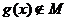 --------------------------4分
--------------------------4分
(2)设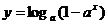
①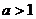 时,由
时,由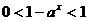 解得:
解得: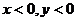
由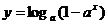 解得其反函数为
解得其反函数为 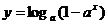 ,
,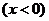 -----------------6分
-----------------6分
②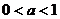 时,由
时,由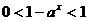 解得:
解得: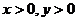
解得函数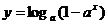 的反函数为
的反函数为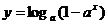 ,
,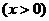 --------------------8分
--------------------8分
∵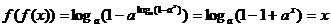
∴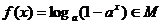 --------------------------------------------------------------------11分
--------------------------------------------------------------------11分
(3)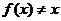 ,
,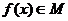 的条件是:
的条件是:
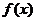 存在反函数
存在反函数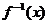 ,且
,且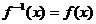 -----------------------------------------------13分
-----------------------------------------------13分
函数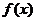 可以是:
可以是:
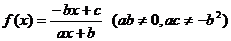 ;
; 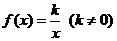 ;
;
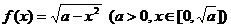 ;
; 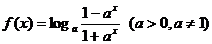 ;
;
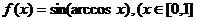 或
或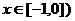 ,
,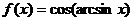 ;
;
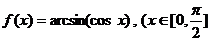 或
或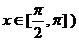 ,
,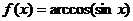 .
.
以“;”划分为不同类型的函数,评分标准如下:
给出函数是以上函数中两个不同类型的函数得3分.
属于以上同一类型的两个函数得1分;
写出的是与(1)、(2)中函数同类型的不得分;
函数定义域或条件错误扣1分.
22.解:(1)由抛物线定义,抛物线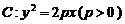 上点
上点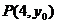 到焦点的距离等于它到准线
到焦点的距离等于它到准线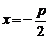 的距离,得
的距离,得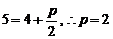 ,
,
所以抛物线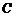 的方程为
的方程为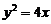 . ----------------------------------------------------------4分
. ----------------------------------------------------------4分
(只要得到抛物线方程,都得4分)
(2)由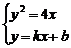 ,得
,得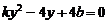 ,(或
,(或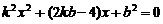 )
)
当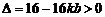 ,即
,即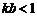 且
且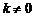 时,
时,
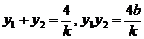 (或
(或 )
)
①由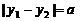 ,即
,即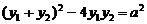 ,得
,得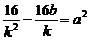 ,
,
所以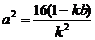 .----------------------------------------------------------------------8分
.----------------------------------------------------------------------8分
②由①知,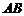 中点
中点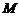 的坐标为
的坐标为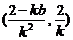 ,点
,点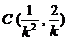 ,
,
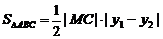
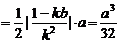 .-------------------------------------12分
.-------------------------------------12分
③由问题②知,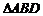 的面积值仅与
的面积值仅与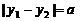 有关,由于
有关,由于
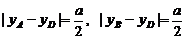 ,所以
,所以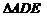 与
与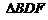 的面积
的面积
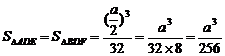 ,设
,设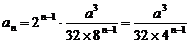 -------14分
-------14分
由题设当中构造三角形的方法,可以将抛物线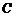 与线段
与线段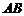 所围成的封闭图形的面积
所围成的封闭图形的面积
看成无穷多个三角形的面积的和,即数列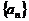 的无穷项和,------------------------16分
的无穷项和,------------------------16分
所以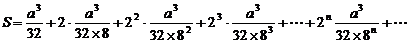
即 ,
,
因此,所求封闭图形的面积为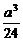 .--------------------------------------------------------18分
.--------------------------------------------------------18分