
网址:http://www.1010jiajiao.com/paper/timu/5151841.html[举报]
11.已知正方体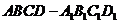 ,
,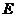 为
为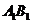 的中点,则异面直线
的中点,则异面直线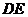 与
与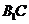 所成角的余弦是
.
所成角的余弦是
.
答 案
一、选择题:DABCD AAACB
二、填空题
11.  ;12. [1,5]; 13.6
;12. [1,5]; 13.6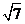 ;14. (0,
;14. (0,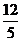 ] ; 15、4;16.① ④.
] ; 15、4;16.① ④.
三、解答题
17.解(1)∵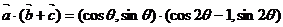
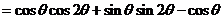 ……………………………
3分
……………………………
3分
=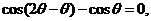
∴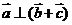 ……………………………………………………………………6分
……………………………………………………………………6分
(2)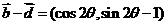 ………………………………………………………7分
………………………………………………………7分
 …………………9分
…………………9分
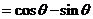 =
=
∵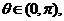 ∴
∴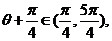 ∴
∴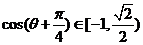
∴ 的值域为
的值域为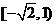 ……………………12分
……………………12分
18.(本小题满分14分)
解:(1)设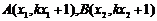 ,则以AB为直径的圆恰好过原点O的充要条件是
,则以AB为直径的圆恰好过原点O的充要条件是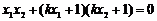 ,即
,即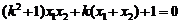 …①……2分
…①……2分
由 消去y得
消去y得 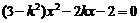 …②
…②
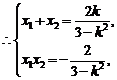 …………………………5分
…………………………5分
将其代入①得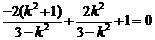 ,解得
,解得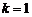 或
或
当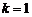 时,方程②为
时,方程②为 ,有两个不等实根;
,有两个不等实根;
当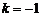 时,方程②为
时,方程②为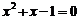 ,有两个不等实根.
,有两个不等实根.
故当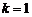 或
或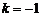 时,以AB为直径的圆恰好过原点O. ………………8分
时,以AB为直径的圆恰好过原点O. ………………8分
(2)若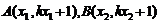 关于直线
关于直线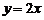 对称,
对称,
则 …………………………10分
…………………………10分
将④整理得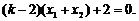 ………………12分
………………12分
因为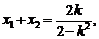 所以
所以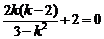 ,解之,得
,解之,得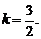 这个结果与③矛盾.
这个结果与③矛盾.
故不存在这样的k,使两点A、B关于直线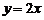 对称. ……………………14分
对称. ……………………14分
18.解:(I)设P(x,y),因为A、B分别为直线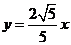 和
和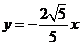 上的点,故可设
上的点,故可设 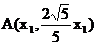 ,
,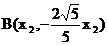 .
.
∵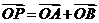 ,
,
∴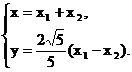 ∴
∴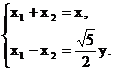 ………………………4分
………………………4分
又 ,
,
∴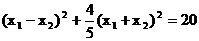 .……………………………………5分
.……………………………………5分
∴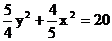 .
.
即曲线C的方程为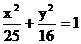 .………………………………………6分
.………………………………………6分
(II) 设N(s,t),M(x,y),则由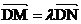 ,可得(x,y-16)=
,可得(x,y-16)=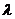 (s,t-16).
(s,t-16).
故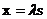 ,
,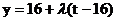 .……………………………………8分
.……………………………………8分
∵M、N在曲线C上,
∴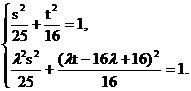 ……………………………………9分
……………………………………9分
消去s得 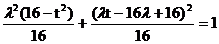 .
.
由题意知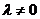 ,且
,且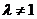 ,
,
解得  .………………………………………………………12分
.………………………………………………………12分
又  , ∴
, ∴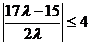 .
.
解得 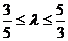 (
(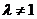 ).
).
故实数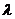 的取值范围是
的取值范围是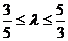 (
(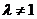 ).………………………………14分
).………………………………14分
19.解:(1) ∵ (
(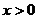 ), ………
2分
), ………
2分
∴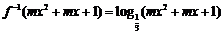 ,由题知,
,由题知,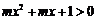 恒成立,
恒成立,
∴10当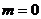 时,
时,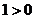 满足题意; ………
3分
满足题意; ………
3分
20当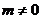 时,应有
时,应有 ,
,
∴实数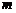 的取值范围为
的取值范围为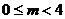 。 ……… 5分
。 ……… 5分
(2) ∵ 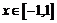 ,∴
,∴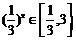 ,
,
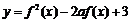
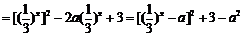 ,……… 7分
,……… 7分
当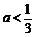 时,
时,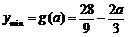 ;
;
当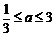 时,
时,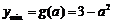 ;
;
当 时,
时,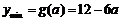 .
.
∴
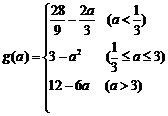 .
…………10分 (错一个扣一分)
.
…………10分 (错一个扣一分)
(3) ∵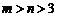 ,∴
,∴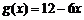 ,在
,在 上是减函数.
上是减函数.
∵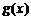 的定义域为
的定义域为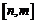 ,值域为
,值域为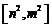 ,
,
∴
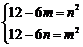 ,
,  …………… 12分
…………… 12分
②-①得: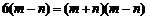 ,
,
∵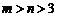 ,∴
,∴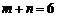 .但这与“
.但这与“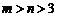 ”矛盾.
”矛盾.
∴满足题意的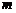 、
、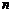 不存在.
………………… 14分
不存在.
………………… 14分
21.解:(1)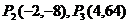 …………………………………………4分
…………………………………………4分
(2)曲线C上点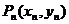 处的切线
处的切线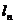 的斜率为
的斜率为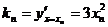 ,
,
故得到切线的方程为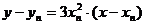 ……………………………………6分
……………………………………6分
联立方程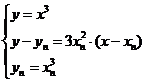 消去y,
消去y,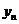 得:
得: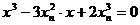
化简得: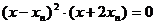 所以:
所以: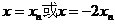 ………………8分
………………8分
由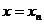 得到点Pn的坐标
得到点Pn的坐标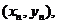 由
由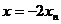 就得到点
就得到点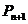 的坐标
的坐标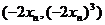 所以:
所以: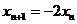 故数列
故数列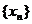 为首项为1,公比为-2的等比数列所以:
为首项为1,公比为-2的等比数列所以: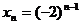 …………………………………………10分
…………………………………………10分
(3)由(2)知: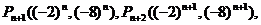
所以直线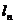 的方程为:
的方程为: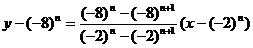
化简得: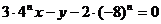 …………………………………………12分
…………………………………………12分
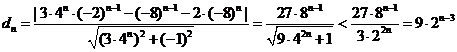
所以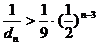 ∴
∴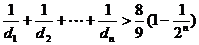 ≥
≥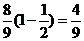 ……16分
……16分