19. 解:∵侧面A1ACC1⊥底面ABC,作A1O⊥AC于点O,
∴A1O⊥平面ABC.
又∠ABC=∠A1AC=60°,且各棱长都相等,
∴AO=1,OA1=OB=,BO⊥AC.
故以O为坐标原点,建立如图所示的空间直角坐标系O-xyz,则
A(0,-1,0),B(,0,0),A1(0,0,),C(0,1,0),
∴.
设平面AB1C的法向量为n=(x,y,1)
则解得n=(-1,0,1).
由cos<>=
而侧棱AA1与平面AB1C所成角,即是向量与平面AB1C的法向量所成锐角的余角,
∴侧棱AA1与平面AB1C所成角的大小为arcsin
(Ⅱ) ∵而
∴
又∵B(,0,0),∴点D的坐标为D(-,0,0).
假设存在点P符合题意,则点P的坐标可设为P(0,y,z).
∴
∵DP∥平面AB1C,n=(-1,0,1)为平面AB1C的法向量,
∴由,得又DP平面AB1C,
故存在点P,使DP∥平面AB1C,其从标为(0,0,),即恰好为A1点.

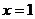 是函数
是函数 的一个极值点(
的一个极值点(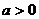 ,e为自然对数的底).
,e为自然对数的底).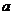 与
与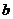 的关系式(用
的关系式(用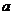 表示
表示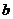 ),并求
),并求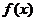 的单调区间;
的单调区间;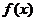 在闭区间
在闭区间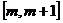 上的最小值为0,最大值为
上的最小值为0,最大值为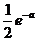 ,且
,且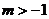 。试求m与
。试求m与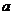 的值.
的值.