
网址:http://www.1010jiajiao.com/paper/timu/5151968.html[举报]
21.解(1)设A,B两点的坐标为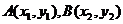 则有
则有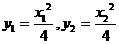 于是
于是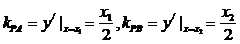 ,由点斜式求得两切线方程:
,由点斜式求得两切线方程:
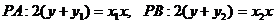 解得P的坐标为
解得P的坐标为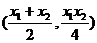
由A,M,B三点共线得: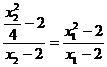 ,
,
即: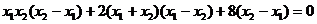 ,由
,由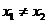 故有
故有
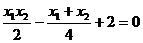 ,故P的轨迹方程为
,故P的轨迹方程为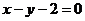
(2)过点M所作垂线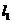 的方程为
的方程为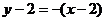 ,即
,即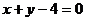 从而交点
从而交点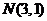
MN的斜率为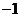 ,若AN,BN的斜率存在,则设为
,若AN,BN的斜率存在,则设为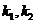 。要证
。要证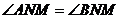 ,只需证
,只需证
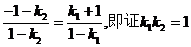 ,而
,而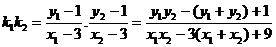
设直线AB的斜率为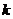 则由:
则由: 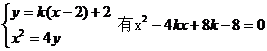
所以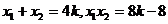
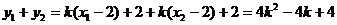
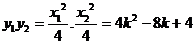 ,代入上式有:
,代入上式有:
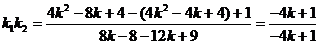
当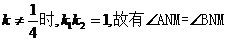
当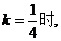 解得A,B两点的坐标分别为
解得A,B两点的坐标分别为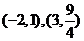 ,知直线AN与BN的斜率一个为零,另一个不存在,也有
,知直线AN与BN的斜率一个为零,另一个不存在,也有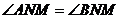 。综上所述,命题得证。
。综上所述,命题得证。