3. (全国卷Ⅰ) 设正项等比数列的首项,前n项和为,且。(Ⅰ)求的通项;(Ⅱ)求的前n项和。
解:(Ⅰ)由 得
即
可得
因为,所以 解得,因而
(Ⅱ)因为是首项、公比的等比数列,故
则数列的前n项和
前两式相减,得
即
[问题2]等差、等比数列的判定问题.P53 T7 例P54 T9
[例]P54 T9(上海卷)已知有穷数列共有2项(整数≥2),首项=2.设该数列的前项和为,且=+2(=1,2,┅,2-1),其中常数>1.
(1)求证:数列是等比数列;(2)若=2,数列满足=(=1,2,┅,2),求数列的通项公式;
(3)若(2)中的数列满足不等式|-|+|-|+┅+|-|+|-|≤4,求的值.
(1) [证明] 当n=1时,a2=2a,则=a;
2≤n≤2k-1时, an+1=(a-1) Sn+2, an=(a-1) Sn-1+2,
an+1-an=(a-1) an, ∴=a, ∴数列{an}是等比数列.
(2) 解:由(1)
得an=2a, ∴a1a2…an=2a=2a=2,
bn=(n=1,2,…,2k).
(3)设bn≤,解得n≤k+,又n是正整数,于是当n≤k时, bn<;
当n≥k+1时, bn>.
原式=(-b1)+(-b2)+…+(-bk)+(bk+1-)+…+(b2k-)
=(bk+1+…+b2k)-(b1+…+bk)
==.
当≤4,得k2-8k+4≤0, 4-2≤k≤4+2,又k≥2,
∴当k=2,3,4,5,6,7时,原不等式成立.

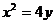 ,过原点作斜率1的直线交抛物线于第一象限内一点
,过原点作斜率1的直线交抛物线于第一象限内一点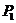 ,又过点
,又过点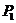 作斜率为
作斜率为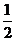 的直线交抛物线于点
的直线交抛物线于点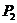 ,再过
,再过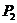 作斜率为
作斜率为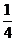 的直线交抛物线于点
的直线交抛物线于点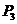 ,
,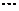 ,如此继续,一般地,过点
,如此继续,一般地,过点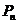 作斜率为
作斜率为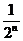 的直线交抛物线于点
的直线交抛物线于点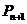 ,设点
,设点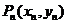 .
.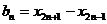 ,求证:数列
,求证:数列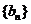 是等比数列.并求数列
是等比数列.并求数列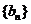 的前
的前 项和为
项和为
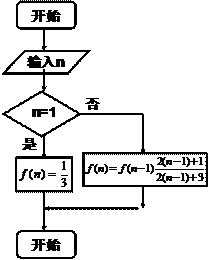 解:(1)因为
解:(1)因为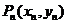 、
、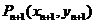 在抛物线上,故
在抛物线上,故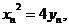 ①
①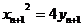 ②,又因为直线
②,又因为直线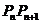 的斜率为
的斜率为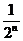 ,即
,即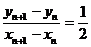 ,①②代入可得
,①②代入可得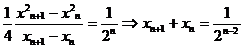
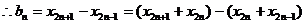
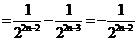 , 故
, 故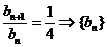 是以
是以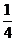
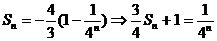 ,
,