18.(山东卷)已知数列{}中,在直线y=x上,其中n=1,2,3….
(Ⅰ)令 (Ⅱ)求数列
(Ⅲ)设的前n项和,是否存在实数,使得数列为等差数列?若存在,试求出.若不存在,则说明理由。
答案与点拨:
1 B 解:由等比数列的性质可得ac=(-1)×(-9)=9,b×b=9且b与奇数项的符号相同,故b=-3,选B
2 B解:在等差数列中,已知∴
d=3,a5=14,=3a5=42,选B.
3 D解:,故选C.
4 D解:由互不相等的实数成等差数列可设a=b-d,c=b+d,由可得b=2,所以a=2-d,c=2+d,又成等比数列可得d=6,所以a=-4,选D
5 A解:依题意,a1+a200=1,故选A
6 (文)C 解:因数列为等比,则,因数列也是等比数列,
则
即,所以,故选择答案C。

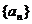 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
.
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
.