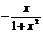例1.(上海春) 设函数.(1)在区间[-2,6]上画出函数的图像;
(2)设集合. 试判断集合和之间的关系,并给出证明;
(3)当时,求证:在区间上,的图像位于函数f(x)图像的上方.
解:(1)(要求列表描点) (2)方程的解分别是和,由于在和[2,5]上单调递减,在[-1,2]和上单调递增,因此 .
由于.
(3)[解法一] 当时,.
,
. 又,
① 当,即时,取,
. , 则.
② 当,即时,取, =.
由
①、②可知,当时,,.
因此,在区间上,的图像位于函数图像的上方.
[解法二] 当时,.由
得, 令 ,
解得 或,
在区间[-1,5]上,当时,的图像与函数f(x)的图像只交于一点;
当时,的图像与函数f(x)的图像没有交点. 如图可知,由于直线过点,当时,直线是由直线绕点逆时针方向旋转得到. 因此,在区间上,的图像位于函数f(x)图像的上方.
例2.(全国卷Ⅱ理17设函数,求使的取值范围.
解:由于是增函数,等价于①
⑴当时,,∴①式恒成立。
⑵当时,,①式化为,即。
⑶当时,,①式无解。 综上,的取值范围为
例3.已知函数(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3, x2=4.
(1)求函数f(x)的解析式; (2)设k>1,解关于x的不等式;
[正确解答](1)将
得
(2)不等式即为
即
①当
②当
③.
例4.(全国II卷)设,函数若的解集为A,,求实数的取值范围。
解:由f(x)为二次函数知,令f(x)=0解得其两根为
由此可知
(i)当时,的充要条件是,即解得
(ii)当时,的充要条件是,即解得
综上,使成立的a的取值范围为
例5.(上海文22)(本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分,计18分)对定义域是、的函数y=f(x)、y=g(x),规定:函数。
(1)若函数,,写出函数的解析式;(2)求问题(1)中函数的值域; (3)若,其中是常数,且,请设计一个定义域为R的函数,及一个的值,使得,并予以证明。
解(3)[解法一]令则
于是
[解法二]令,
则
于是
例6.设的值域为[-1,4],求a、b的值.
例7:已知函数f(x)=,x∈[1,+∞,(1)当a=0.5时,求函数f(x)的最小值
(2)若对任意x∈[1,+∞,f(x)>0恒成立,试求实数a的取值范围
(1)解
当a=时,f(x)=x++2
∵f(x)在区间[1,+∞上为增函数,∴f(x)在区间[1,+∞上的最小值为f(1)=
(2)解法一
在区间[1,+∞上,f(x)= >0恒成立x2+2x+a>0恒成立
设y=x2+2x+a,x∈[1,+∞,∵y=x2+2x+a=(x+1)2+a-1递增,
∴当x=1时,ymin=3+a,当且仅当ymin=3+a>0时,函数f(x)>0恒成立,故a>-3
解法二
f(x)=x++2,x∈[1,+∞
当a≥0时,函数f(x)的值恒为正; 当a<0时,函数f(x)递增,故当x=1时,f(x)min=3+a,
当且仅当f(x)min=3+a>0时,函数f(x)>0恒成立,故a>-3
点评 本题主要考查函数的最小值以及单调性问题,着重于学生的综合分析能力以及运算能力
解题的关健是把求a的取值范围的问题转化为函数的最值问题.通过求f(x)的最值问题来求a的取值范围,体现了转化的思想与分类讨论的思想

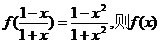 的解析式
的解析式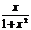 B.
B.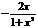 C.
C.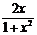 D.
D.