网址:http://www.1010jiajiao.com/paper/timu/5152766.html[举报]
6、设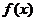 是可导函数,且
是可导函数,且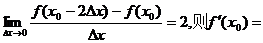
A.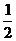 B.-1 C.0 D.-2
B.-1 C.0 D.-2
十三、导数参考答案
1、B;2、D;3、C;4、B;5、A;6、B;7、A;8、-26;9、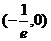 ;10、C
;10、C
11、A;12、B;13、B.
14. 解:设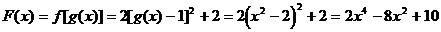
则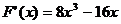 ,令
,令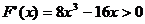
解得: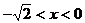 ,或
,或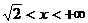 ,由于
,由于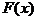 是R上的连续函数,所以函数
是R上的连续函数,所以函数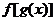 的单调递增区间为
的单调递增区间为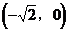 和
和
15、解. (1)∵函数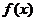 图象关于原点对称,∴对任意实数
图象关于原点对称,∴对任意实数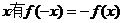 ,
,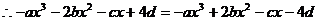 ,即
,即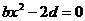 恒成立
恒成立
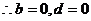
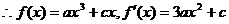 ,
,
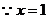 时,
时,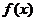 取极小值
取极小值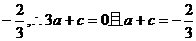 ,
,
解得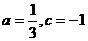
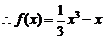
(2)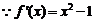 令
令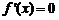 得
得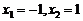
|
x |
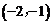 |
 |
 |
1 |
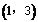 |
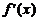 |
+ |
0 |
- |
0 |
+ |
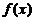 |
↑ |
极大值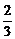 |
↓ |
极小值-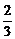 |
↑ |
又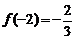 ,
, 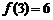 ,故当
,故当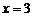 时,
时,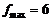 .
.
16、解:(I)设该学生从家出发,先乘船渡河到达公路上某一点P(x,0)
(0≤x≤d),再乘公交车去学校,所用的时间为t,则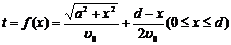 .
.
令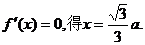
且当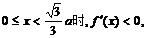
当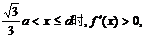
当 时,所用的时间最短,最短时间为:
时,所用的时间最短,最短时间为:
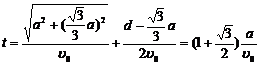 .
.
答:当d=2a时,该学生从家出发到达学校所用的最短时间是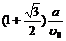 .
.
(II)由(I)的讨论可知,当d=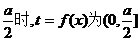 上的减函数,所以当
上的减函数,所以当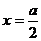 时,
时,
即该学生直接乘船渡河到达公路上学校,所用的时间最短
最短的时间为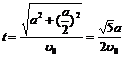
答:当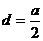 时,该学生从家出发到达学校所用的最短时间是
时,该学生从家出发到达学校所用的最短时间是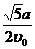 .
.
17、解: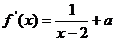 ,
,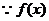 在
在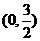 上是增函数
上是增函数
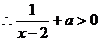 在
在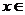
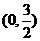 上恒成立 ,
上恒成立 , 恒成立
恒成立
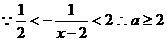 ,
,
设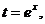 则
则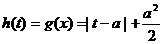
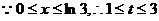
当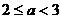 时,
时,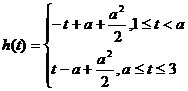
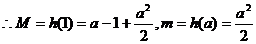
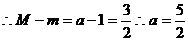
当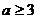 时,
时,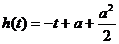
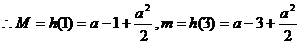
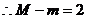 不符题意
不符题意
综上,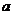 的取值为
的取值为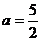
18、(1)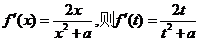 ,切线
,切线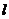 的方程:
的方程: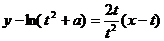
(2)令x=0,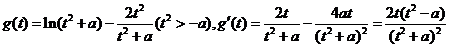
①
当a>0时,由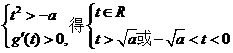 ,
,
②当a=0时,由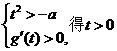
③当a<0时,
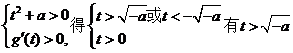
综合①②③当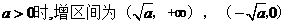
当a=0时,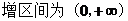
当a<0时,