
网址:http://www.1010jiajiao.com/paper/timu/5152846.html[举报]
5.(人教A版第43页A组第6题)奇偶性
变式1: 解:函数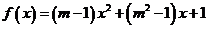 是偶函数 Þ
是偶函数 Þ 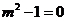 Þ
Þ 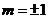 ,
,
当 时,
时,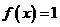 是常数;当
是常数;当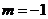 时,
时,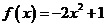 ,在区间
,在区间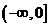 上
上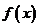 是增函数,故选D.
是增函数,故选D.
变式2:解:根据题意可知应有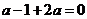 且
且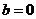 ,即
,即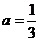 且
且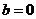 ,∴点
,∴点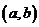 的坐标是
的坐标是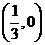 .
.
变式3: 解:(I)当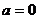 时,函数
时,函数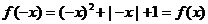 ,此时,
,此时,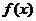 为偶函数;
为偶函数;
当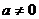 时,
时,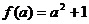 ,
,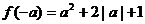 ,
,
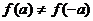 ,
,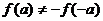 ,此时
,此时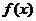 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(II)(i)当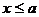 时,
时, ,
,
若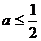 ,则函数
,则函数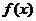 在
在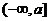 上单调递减,从而函数
上单调递减,从而函数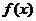 在
在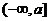 上的最小值为
上的最小值为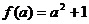 .
.
若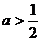 ,则函数
,则函数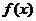 在
在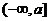 上的最小值为
上的最小值为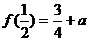 ,且
,且 .
.
(ii)当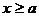 时,函数
时,函数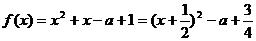 ,
,
若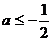 ,则函数
,则函数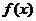 在
在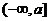 上的最小值为
上的最小值为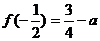 ,且
,且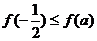 ,
,
若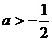 ,则函数
,则函数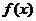 在
在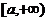 上单调递增,从而函数
上单调递增,从而函数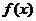 在
在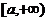 上的最小值为
上的最小值为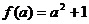 .
.
综上,当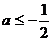 时,函数
时,函数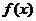 的最小值为
的最小值为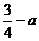 ;
;
当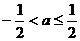 时,函数
时,函数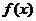 的最小值为
的最小值为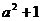 ;
;
当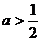 时,函数
时,函数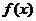 的最小值为
的最小值为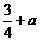 .
.