
网址:http://www.1010jiajiao.com/paper/timu/5152849.html[举报]
8.(北师大版第54页B组第5题)恒成立问题
变式1: 解:(I) 函数 f (x) 的定义域为 R,即不等式a x 2 + 2x + 1 > 0 的解集为 R,
∴应有 Þ a > 1,
∴ 实数 a 的取值范围是(1,+¥) .
(II) 函数 f (x) 的值域为 R,即a x 2 + 2x + 1 能够取 (0,+¥) 的所有值.
1° 当 a = 0 时,a x 2 + 2x + 1 = 2x + 1满足要求;
2° 当 a ≠ 0 时,应有 Þ 0 < a≤1.
∴ 实数 a 的取值范围是[0,1] .
变式2: 解法一:(转化为最值)
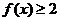 在
在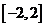 上恒成立,即
上恒成立,即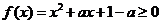 在
在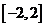 上恒成立.
上恒成立.
⑴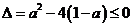 ,
, 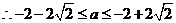 ;
;
⑵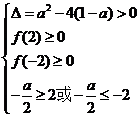 ,
,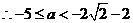 .
.
综上所述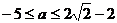 .
.
解法二:(运用根的分布)
⑴当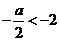 ,即
,即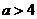 时,应有
时,应有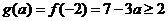 , 即
, 即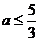 ,
,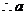 不存在;
不存在;
⑵当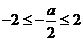 ,即
,即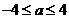 时,应有
时,应有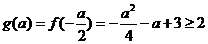 ,
,
即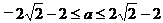 ,
,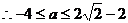 ;
;
⑶当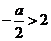 ,即
,即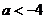 时,应有
时,应有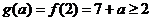 ,即
,即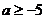 ,
, 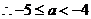
综上所述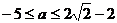 .
.
变式3: 证明:(I) 依题意,f (sin ) = f (1)≥0,f (2 + cos p) = f (1)≤0,
∴ f (1) = 0 Þ 1 + b + c = 0 Þ b + c = -1,
(II) 由 (I) 得: f (x) = x 2-(c + 1) x + c (*)
∵ f (2 + cos b )≤0 Þ (2 + cos b ) 2-(c + 1) (2 + cos b ) + c≤0
Þ (1 + cos b ) [c-(2 + cos b )]≥0,对任意 b 成立.
∵ 1 + cos b ≥0 Þ c≥2 + cos b ,
∴ c≥(2 + cos b )max = 3.
(III) 由 (*) 得:f (sin a ) = sin 2a-(c + 1) sin a + c,
设 t = sin a ,则g(t) = f (sin a ) = t 2-(c + 1) t + c,-1≤t≤1,
这是一开口向上的抛物线,对称轴为 t = ,
由 (II) 知:t≥= 2,
∴ g(t) 在 [-1,1] 上为减函数.
∴ g(t)max = g(-1) = 1 + (c + 1) + c = 2c + 2 = 8,
∴ c = 3
∴ b = -c-1 = -4.