
网址:http://www.1010jiajiao.com/paper/timu/5152874.html[举报]
例1(1)已知c<b<a,且ac<0,那么下列选项中一定成立的是
(A)ab>ac (B)c(b-a)<0 (C)cb2<ab2 (D)ac(a-c)>0
(2)若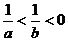 。则下列不等式(1)a+b<ab (2)
。则下列不等式(1)a+b<ab (2)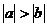 (3)a<b (4)
(3)a<b (4)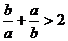 中,正确的有____个
中,正确的有____个
本题是运用不等式性质求解的基础题,(1)题选A (2)题填2。
例2不等式3x2-log ax<0在区间(0,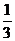 )内恒成立,求a的取值范围。
)内恒成立,求a的取值范围。
本题数形结合,借助两个函数图象比较两函数值的大小,答案: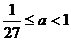
例3已知f(x)=x2-2ax+2,当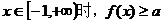 恒成立,求a的取值范围。
恒成立,求a的取值范围。
分析:f(x)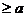 恒成立等价于f(x)min
恒成立等价于f(x)min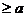 ,问题化归为求f(x)在
,问题化归为求f(x)在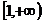 上的最小值g(a),再解不等式g(a)
上的最小值g(a),再解不等式g(a) 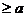 ,可求a的取值范围。
,可求a的取值范围。
例4.在约束条件 的取值范围是
.
的取值范围是
.
分析:画出约束条件所表示的可行域,目标函数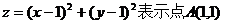 和可行域内点的距离的平方,最小值为点A到直线
和可行域内点的距离的平方,最小值为点A到直线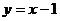 的距离的平方,最大值在点(2,0)处取得。答案为
的距离的平方,最大值在点(2,0)处取得。答案为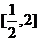 。
。
例5.已知二次函数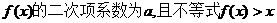 的解集为(1,2)
的解集为(1,2)
(1)若方程 有两个相等的实根,求
有两个相等的实根,求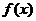 的解析式;
的解析式;
(2)若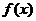 的最大值大于1,求a的取值范围.
的最大值大于1,求a的取值范围.
解:(1)不等式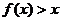 的解集为(1,2)
的解集为(1,2)


(2)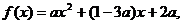
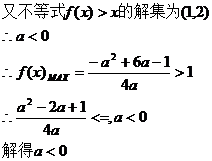
本题涉及“三个二次”,要引起足够重视。
例6.已知函数f(x)=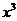 -
-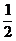 x2+bx+c.(1)若f (x)有极值,求b的取值范围;
x2+bx+c.(1)若f (x)有极值,求b的取值范围;
(2)当f (x)在x=1处取得极值时,
①若当x∈[-1,2]时,f (x)<c2恒成立,求c的取值范围;
②证明:对[-1,2]内的任意两个值x1,x2,都有|f (x1)-f (x2)|<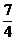 .
.
解:(1)∵f(x)=x3-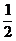 x2+bx+c,
∴f `(x)=3x2-x+b
x2+bx+c,
∴f `(x)=3x2-x+b
要使f(x)有极值,则f `(x)=3x2-x+b=0有实数解
从而△=1-12b≥0,∴b≤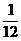 而当b=
而当b=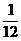 时,函数在R上严格递增,∴b<
时,函数在R上严格递增,∴b<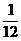
(2)∵f(x)在x=1处取得极值 ∴f `(1)=3-1+b=2+b=0 ∴b=-2
①∴f(x)=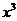 -
-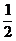 x2-2x+c
x2-2x+c
∵f `(x)=3x2-x-2=(3x+2)(x-1)
∴当x∈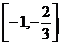 时,f `(x)>0,函数单调递增
时,f `(x)>0,函数单调递增
当x∈(-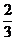 ,1)时,f `(x)<0,函数单调递减
,1)时,f `(x)<0,函数单调递减
∴当x=-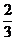 时,f (x)有极大值
时,f (x)有极大值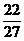 +c
+c
又f
(2)=2+c >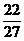 +c,
f (-1)=
+c,
f (-1)=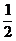 +c<
+c<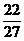 +c
+c
∴x∈[-1,2]时,f (x)最大值为f (2)=2+c
∴c2>2+c ∴c<-1或c>2
②由上可知,当x=1时,f(x)有极小值-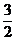 +c
+c
又f (2)=2+c>-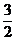 +c, f (-1)=
+c, f (-1)=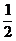 +c>-
+c>-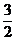 +c
+c
∴x∈[-1,2]时,f (x)的最小值为-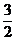 +c
+c
∴|f (x1)-f (x2)|<|fmax(x)-fmax(x)|=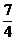 ,故结论成立.
,故结论成立.
涉及函数的增减区间,最大值与最小值与不等式也紧密相关。
专题练习参考答案:
C A D B B D
9. 6 10. 2
11. (-∞,-1) 12. 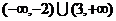 13.
13. 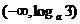
14. (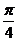 ,1)
,1)
15. 解:不等式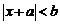 的解是
的解是 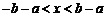 ,依题设得
,依题设得
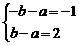 解这个方程组得
解这个方程组得 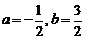
可知不等式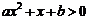 为
为 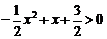 即
即 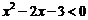
解得 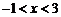 ,故不等式
,故不等式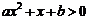 的解集是
的解集是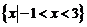
16. 解:(1)∵ f (x)<0 Û |x-a|<ax, 0<a<1
当x≥a时,原不等式 Û (1-a)x<a Û x<,即a≤x<,
当x<a时,原不等式 Û (1+a)x>a Û x>,<x<a.
∴ 不等式的解集为{x|<x<}.
(2)f (x) = |x-a|-ax = ,
可知,当x≥a时函数单调递增,当x<a时函数单调递减,
所以函数f(x)有最小值f (a) = -a2
17. 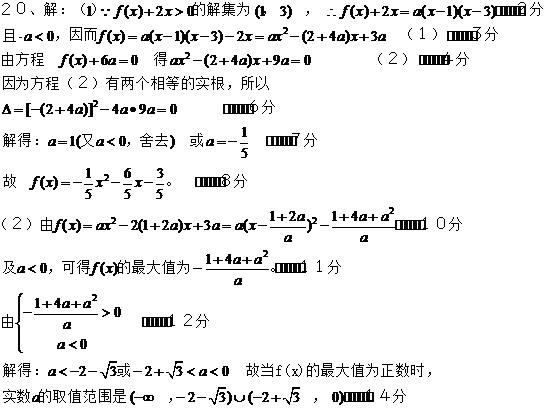
18. 解:(Ⅰ)当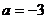 时,
时,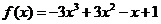
∵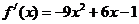

∴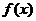 在
在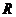 上是减函数
上是减函数
(Ⅱ)∵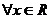 不等式
不等式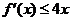 恒成立
恒成立
即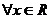 不等式
不等式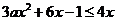 恒成立
恒成立
∴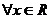 不等式
不等式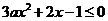 恒成立
恒成立
当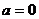 时,
时,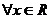
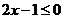 不恒成立
不恒成立
当 时,
时,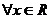 不等式
不等式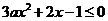 恒成立
恒成立
即
∴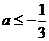
当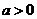 时,
时,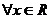 不等式
不等式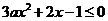 不恒成立
不恒成立
综上所述,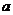 的取值范围是
的取值范围是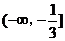
19. 解 (1)∵f(x)是二次函数,f(x)<0的解集是(0,5)
∴可设f(x)=ax(x-5) (a>0)
因为f(x)图象的对称轴为x=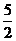 ,∴f(x)在区间[-1,4]上的最大值是f(-1)=6a,
,∴f(x)在区间[-1,4]上的最大值是f(-1)=6a,
由已知得6a=12,∴a=2 ∴f(x)=2x(x-5)=2x2-10x (x∈R)
(2)方程f(x)+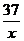 =0等价于方程2x3-10x2+37=0
=0等价于方程2x3-10x2+37=0
设h(x)= 2x3-10x2+37.则h(x)=6x2-20x=2x(3x-10)
当x∈(0,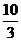 ) 时,
) 时,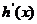 <0,h(x)是减函数,
<0,h(x)是减函数,
当x∈(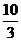 ,+∞) 时,
,+∞) 时, 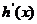 >0,h(x)是增函数,
>0,h(x)是增函数,
∵h(3)=1>0,h(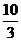 )=
)=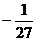 <0,h(4)=5>0∴方程h(x)=0在区间(3,
<0,h(4)=5>0∴方程h(x)=0在区间(3,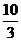 ),(
),(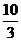 ,4)内分别有唯一实数根,而在区间(0,3),(4,+∞)内没有实数根。
,4)内分别有唯一实数根,而在区间(0,3),(4,+∞)内没有实数根。
∴存在唯一的自然数m=3,使得方程f(x)+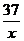 =0 在区间(m,m+1)内有且
=0 在区间(m,m+1)内有且
只有两个不同的实数根。