
网址:http://www.1010jiajiao.com/paper/timu/5152887.html[举报]
13.设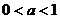 ,函数
,函数 ,则使
,则使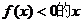 取值范围是____________
取值范围是____________
专题练习参考答案:
C A D B B D
9. 6 10. 2
11. (-∞,-1) 12. 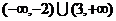 13.
13. 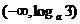
14. (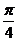 ,1)
,1)
15. 解:不等式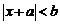 的解是
的解是 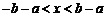 ,依题设得
,依题设得
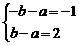 解这个方程组得
解这个方程组得 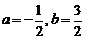
可知不等式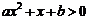 为
为 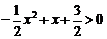 即
即 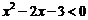
解得 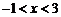 ,故不等式
,故不等式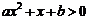 的解集是
的解集是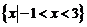
16. 解:(1)∵ f (x)<0 Û |x-a|<ax, 0<a<1
当x≥a时,原不等式 Û (1-a)x<a Û x<,即a≤x<,
当x<a时,原不等式 Û (1+a)x>a Û x>,<x<a.
∴ 不等式的解集为{x|<x<}.
(2)f (x) = |x-a|-ax = ,
可知,当x≥a时函数单调递增,当x<a时函数单调递减,
所以函数f(x)有最小值f (a) = -a2
17. 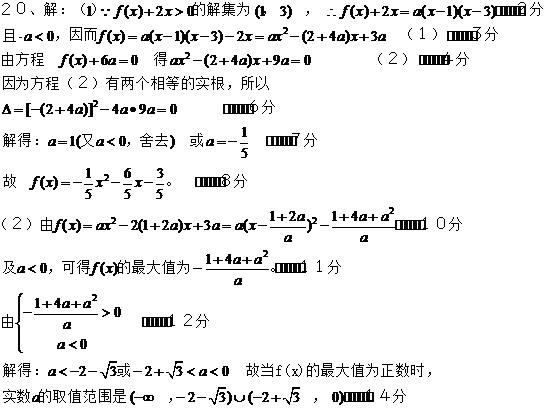
18. 解:(Ⅰ)当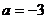 时,
时,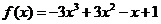
∵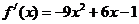

∴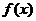 在
在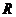 上是减函数
上是减函数
(Ⅱ)∵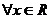 不等式
不等式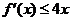 恒成立
恒成立
即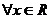 不等式
不等式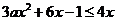 恒成立
恒成立
∴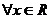 不等式
不等式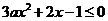 恒成立
恒成立
当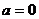 时,
时,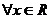
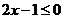 不恒成立
不恒成立
当 时,
时,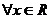 不等式
不等式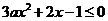 恒成立
恒成立
即
∴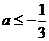
当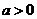 时,
时,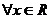 不等式
不等式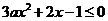 不恒成立
不恒成立
综上所述,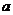 的取值范围是
的取值范围是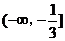
19. 解 (1)∵f(x)是二次函数,f(x)<0的解集是(0,5)
∴可设f(x)=ax(x-5) (a>0)
因为f(x)图象的对称轴为x=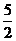 ,∴f(x)在区间[-1,4]上的最大值是f(-1)=6a,
,∴f(x)在区间[-1,4]上的最大值是f(-1)=6a,
由已知得6a=12,∴a=2 ∴f(x)=2x(x-5)=2x2-10x (x∈R)
(2)方程f(x)+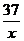 =0等价于方程2x3-10x2+37=0
=0等价于方程2x3-10x2+37=0
设h(x)= 2x3-10x2+37.则h(x)=6x2-20x=2x(3x-10)
当x∈(0,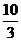 ) 时,
) 时,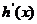 <0,h(x)是减函数,
<0,h(x)是减函数,
当x∈(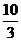 ,+∞) 时,
,+∞) 时, 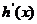 >0,h(x)是增函数,
>0,h(x)是增函数,
∵h(3)=1>0,h(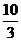 )=
)=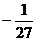 <0,h(4)=5>0∴方程h(x)=0在区间(3,
<0,h(4)=5>0∴方程h(x)=0在区间(3,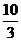 ),(
),(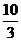 ,4)内分别有唯一实数根,而在区间(0,3),(4,+∞)内没有实数根。
,4)内分别有唯一实数根,而在区间(0,3),(4,+∞)内没有实数根。
∴存在唯一的自然数m=3,使得方程f(x)+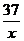 =0 在区间(m,m+1)内有且
=0 在区间(m,m+1)内有且
只有两个不同的实数根。