+(200÷30)＝146
所以，符合条件的数共有200－146＝54(个)
点评：分析200个数分为两类，即满足题设条件的和不满足题设条件的两大类，而不满足条件的这一类标准明确而简单，可考虑用扣除法。
题型7：集合综合题
例11．(1999上海，17)设集合A={x||x－a|<2}，B={x|<1}，若AB，求实数a的取值范围。
解：由|x－a|<2，得a－2<x<a+2，所以A={x|a－2<x<a+2}。
由<1，得<0，即－2<x<3，所以B={x|－2<x<3}。
因为AB，所以，于是0≤a≤1。
点评：这是一道研究集合的包含关系与解不等式相结合的综合性题目。主要考查集合的概念及运算，解绝对值不等式、分式不等式和不等式组的基本方法。在解题过程中要注意利用不等式的解集在数轴上的表示方法.体现了数形结合的思想方法。
例12．已知{an}是等差数列，d为公差且不为0，a1和d均为实数，它的前n项和记作Sn,设集合A={(an,)|n∈N*},B={(x,y)| x2－y2=1,x,y∈R}。
试问下列结论是否正确，如果正确，请给予证明；如果不正确，请举例说明：
(1)若以集合A中的元素作为点的坐标，则这些点都在同一条直线上；
(2)A∩B至多有一个元素；
(3)当a1≠0时，一定有A∩B≠。
解：(1)正确；在等差数列{an}中，Sn=,则(a1+an),这表明点(an,)的坐标适合方程y(x+a1),于是点(an,
)均在直线y=x+a1上。
(2)正确；设(x,y)∈A∩B,则(x,y)中的坐标x,y应是方程组的解，由方程组消去y得：2a1x+a12=－4(*)，
当a1=0时，方程(*)无解，此时A∩B=；
当a1≠0时，方程(*)只有一个解x=,此时，方程组也只有一解,故上述方程组至多有一解。
∴A∩B至多有一个元素。
(3)不正确；取a1=1，d=1，对一切的x∈N*，有an=a1+(n－1)d=n>0, >0，这时集合A中的元素作为点的坐标，其横、纵坐标均为正，另外，由于a1=1≠0 如果A∩B≠，那么据(2)的结论，A∩B中至多有一个元素(x0,y0),而x0=＜0,y0=＜0，这样的(x0,y0)A,产生矛盾，故a1=1,d=1时A∩B=，所以a1≠0时，一定有A∩B≠是不正确的。
点评：该题融合了集合、数列、直线方程的知识，属于知识交汇题。
变式题：解答下述问题：
(Ⅰ)设集合，,求实数m的取值范围.
分析：关键是准确理解 的具体意义，首先要从数学意义上解释 的意义，然后才能提出解决问题的具体方法。
解：
的取值范围是UM={m|m<-2}.
(解法三)设这是开口向上的抛物线，，则二次函数性质知命题又等价于
注意，在解法三中，f(x)的对称轴的位置起了关键作用，否则解答没有这么简单。
(Ⅱ)已知两个正整数集合A={a1,a2,a3,a4},
、B.
分析：命题中的集合是列举法给出的，只需要根据“交、并”的意义及元素的基本性质解决，注意“正整数”这个条件的运用，
(Ⅲ)
分析：正确理解
要使,
由
当k=0时，方程有解,不合题意；
当①
又由
由②，
由①、②得
∵b为自然数，∴b=2，代入①、②得k=1
点评：这是一组关于集合的“交、并”的常规问题，解决这些问题的关键是准确理解问题条件的具体的数学内容，才能由此寻求解决的方法。
题型6：课标创新题
例13．七名学生排成一排，甲不站在最左端和最右端的两个位置之一，乙、丙都不能站在正中间的位置，则有多少不同的排法？
解：设集合A={甲站在最左端的位置}，
B={甲站在最右端的位置}，
C={乙站在正中间的位置}，
D={丙站在正中间的位置}，
则集合A、B、C、D的关系如图所示，
∴不同的排法有种.
点评：这是一道排列应用问题，如果直接分类、分步解答需要一定的基本功，容易错，若考虑运用集合思想解答，则比较容易理解。上面的例子说明了集合思想的一些应用，在今后的学习中应注意总结集合应用的经验。
例14．A是由定义在上且满足如下条件的函数组成的集合：①对任意，都有 ； ②存在常数，使得对任意的，都有
(1)设，证明：
(2)设,如果存在,使得,那么这样的是唯一的;
(3)设,任取,令证明:给定正整数k,对任意的正整数p,成立不等式。
解：
对任意,,,,所以
对任意的，
，
，
所以0<,
令=，
，
所以
反证法：设存在两个使得,。
则由，
得，所以，矛盾，故结论成立。
，
所以
+…
。
点评：函数的概念是在集合理论上发展起来的，而此题又将函数的性质融合在集合的关系当中，题目比较新颖。
、
、
、
、=、
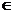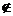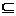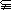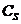A、∪，∩等等；