网址：http://www.1010jiajiao.com/paper/timu/5153563.html[举报]
1．(人教A版选修2-3第22页例4)
用 0 到 9 这 10 个数字，可以组成多少个没有重复数字的三位数 ？
变式1： 由1，4，5，x可组成没有重复数字的四位数，若所有这些四位数的各位数字之和为288，则x＝ ．
[解析]：(1+4+5+x)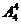
=288，解得10+x=12．
[答案]：x=2．
变式2：在由数字1，2，3，4，5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有 ( )
(A)56个 (B)57个 (C)58个 (D)60个
[解答]解法一：(直接法)
当首位排2，次位排3时，有A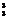
-1种；次位排4、5时有2 A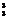种，共计17种；
当首位排3，A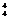
种，共计24种；
当首位排4，次位排3时，有A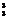-1种；次位排1、2时有2 A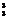种，共计17种；
以上总计17+24+17=58种。
解法二：(间接法)
不作限定时有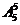
=120种；
当首位排1或5时，各有A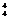种，共计48种不满足要求；
当首位排2，次位排1时，有A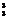种；而次位排3时有1种，共计7种不满足要求；
当首位排4，次位排5时，有A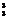种；而次位排3时有1种，共计7种不满足要求；
因此共有120-48-7-7=58种排法，即58个数．
变式3：给定数字0、1、2、3、5、9每个数字最多用一次
(1)可能组成多少个四位数？
(2)可能组成多少个四位奇数？
(3)可能组成多少个四位偶数？
(4)可能组成多少个自然数？
[分析]：注意0不能放在首位，还要注意个位数字，方法多种多样，利用特殊优先法，即特殊的元素，特殊的位置优先考虑．
[解答](1)解法一：从“位置”考虑，由于0不能放在首位，因此首位数字只能有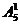
种取法，其余3个数位可以从余下的5个数字(包括0)中任取3个排列，所以可以组成
个四位数；
解法二：从“元素”考虑，组成的四位数可以按有无数字0分成两类，有数字0的有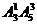
个，无数字0的有
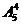个，所以共组成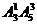+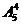=300个四位数；
解法三：“排除法”从6个元素中取4个元素的所有排列中，减去0在首位上的排列数即为所求，所以共有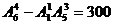
个四位数；
(2)从“位置”考虑，个位数字必须是奇数有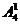
种排法，由于0不能放在首位，因此首位数字只能有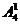种取法，其余两个数位的排法有
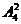，所以共有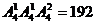
个四位奇数；
(3)解法一：由(1)(2)知共有300-192=108个四位偶数；
解法二：从“位置”考虑，按个位数字是否为0分成两种情况，0在个位时，有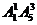
个四位偶数；2在个位时，有
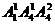个四位偶数，所以共有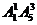+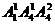=108个四位偶数；
(4)一位数：有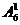
=6个；
两位数：有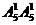
=25个；
三位数：有
=100个；
四位数：有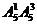
=300个；
五位数：有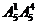
=600个；
六位数：有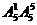
=600个；
所以共有6+25+100+300+600+600=1631个自然数．
[点评]解有条件限制的排列问题思路：①正确选择原理；②处理好特殊元素和特殊位置，先让特殊元素占位，或特殊位置选元素；③再考虑其余元素或其余位置；④数字的排列问题，0不能排在首位．