
网址:http://www.1010jiajiao.com/paper/timu/5153634.html[举报]
11.市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律:该商品的价格每上涨x%(x > 0),销售数量就减少kx%(其中k为正常数)。目前,该商品定价为a元,统计其销售数量为b个。
(Ⅰ)当k= 时,该商品的价格上涨多少,就能使销售的总金额达到最大?(Ⅱ)在适当的涨价过程中,求使销售总金额不断增加时,k的取值范围。
时,该商品的价格上涨多少,就能使销售的总金额达到最大?(Ⅱ)在适当的涨价过程中,求使销售总金额不断增加时,k的取值范围。
[参考答案]
联想与激活(5)
1.C 联想:(1)A
(2)y = -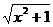 (x≥0) (3)9
(x≥0) (3)9
(4)t≤ (5)D
(6)C
(5)D
(6)C
2.C 联想:(1)①②③ (2)a
=  (3)A
(4)
(3)A
(4)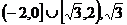
3.B 联想:(1)B (2)A (3)4 (4)12
4.A 联想:(1)C (2)x+y
= 3 (3)y2-x2
= 
(4)-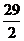 (5)
(5)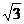 ,1200
(6)-34
,1200
(6)-34
5.B 联想:(1)B (2)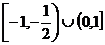 (3)
(3)
6.A 联想:(1)A (2)3 (3)A (4)D
7.D 联想:(1)A (2)B
(3)C (4)-3x4-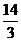 x3
(5)[ 1,
x3
(5)[ 1,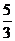 ]
]
8.B 联想:(1)B (2)10 (3)C
9.C 联想:(1)1 (2)8
10.C 联想: D
11. 2联想:(1)( x-1)2 = 4(y+1) (2)( y+6 )2 = 8(x+6)
12.解:(I)设F(C,O)(C>O)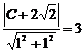 C=
C=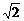 又b=1,
∴a=3
又b=1,
∴a=3
∴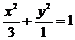
(II)假设这样的直线存在,交于两点(x1,y1)(x2,y2)
则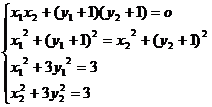
利用中点在椭圆的内部求出k的范围是(-1,0)∪(0,1)
联想与激活(6)
1.B
联想:(1)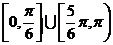 (2)B (3)C
(2)B (3)C
2.B 联想:(1)B (2)0<a<1时,x>1;a>1时,0<x<1
(3)a>1时,x∈(-1,0);0<a<1时,x∈(-2,-1)
3.A 联想:(1)D (2)A (3)C (4)m>7
4.B
联想:(1)D (2)cos4x或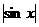 (3)f
(m-1)>0
(3)f
(m-1)>0
5.A
联想:(1)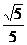 (2)
(2)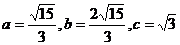 (3)
(3)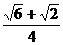
(4)①A=45°,B=60°,C=75°
②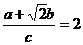
设A=60°-α,C=60°+α
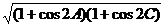 =2cosAcosC=cos(A+C)+cos(A-C)=cos120°+cos2α=
=2cosAcosC=cos(A+C)+cos(A-C)=cos120°+cos2α=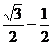
∴cos2α=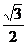 α=15°
∴A=45°,C=75°
α=15°
∴A=45°,C=75°
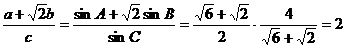
(5) ①cosa=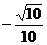 ②f-1(
②f-1(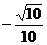 )=
)=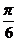
2a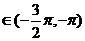 ∴cos2
∴cos2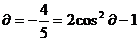
2cos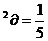 cos
cos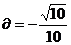
f(x)=-2cos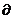 sinX+2cos
sinX+2cos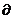 ∴-2cos
∴-2cos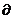 sinx+2cos
sinx+2cos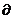 =-
=-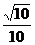
∴-2sinx+2=1
sinx= x=
x=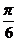 f-1(-
f-1(-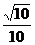 )=
)=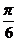
6. C 联想:(1)C (2)B (3)93
(4)an=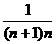 (5) ①{bn}为A.P
(5) ①{bn}为A.P
bn≠o,
2b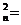 anan+1, an+1=bnbn+1,an=bn-1bn
anan+1, an+1=bnbn+1,an=bn-1bn
∴2b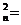 bn(bn-1+bn+1)
2bn = bn-1+bn+1
bn(bn-1+bn+1)
2bn = bn-1+bn+1
②2b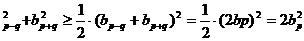
③3 a1+a2=2b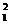 ∴a2=3
a2=b1b2 b2=
∴a2=3
a2=b1b2 b2=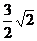
∴d=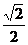 ∴bn=
∴bn=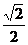 n ∴an=bn-1bn=
n ∴an=bn-1bn=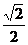 (n-1).
(n-1).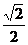 n=
n=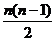 (n≥2)
(n≥2)
∴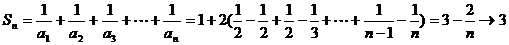
7.B
联想:(1)C (2)19
(3)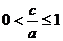 (4)5,5
(4)5,5
8.- 联想:I.圆
II.
联想:I.圆
II.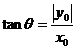
设p(x,y) 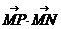 =2x+2
=2x+2
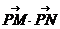 =x2-1+y2
=x2-1+y2
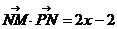 ∴2x=x2-1+y2
(x-1)2+y2=2
∴2x=x2-1+y2
(x-1)2+y2=2
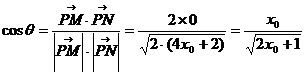
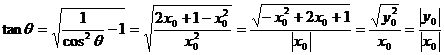 (x0≥0)
(x0≥0)
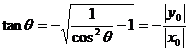 (x0<0
(x0<0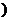 ∴
∴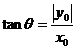
9.D
联想:(1)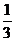 (2)D
(3)
(2)D
(3)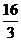 (4)
(4) ≤e<1
≤e<1
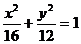
①B(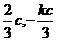 )
∴
)
∴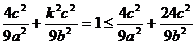 ∴4e4-37e2+9≤0
∴4e4-37e2+9≤0
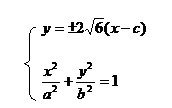
 ≤e≤3又e<1
∴
≤e≤3又e<1
∴ ≤e≤1
≤e≤1
②e=
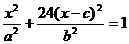
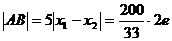 ∴
∴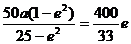 a=4
a=4
∴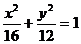
10.B
联想:(1)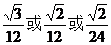 (答案不唯一) (2)A (3)B
(答案不唯一) (2)A (3)B
(4)I:证:正△ABC中,作BC边上高AF,交BC于F
交DE于G,则AG⊥DE,DE⊥FG。
∴A′G⊥DE,FG⊥DE A′G交FG于面A′GF ∴面DE⊥A′GF
DE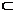 面BCED
∴面A′GF⊥面BCED
面BCED
∴面A′GF⊥面BCED
Ⅱ:过A′作A′M⊥AF于M,连EM。
面A′GF⊥面BCED A′M⊥AF 易知A′M⊥面ABC 又A′E⊥BD
∴EM⊥AB 则AM=2MG 如图
 A′G = AG =
3MG ∴cos∠A′GM
=
A′G = AG =
3MG ∴cos∠A′GM
= 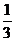
∠A′GM
= π-arccos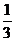
A′G⊥DE , FG⊥DE ∴∠A′GF为所求二面角的平面角
∴所求二面角为π-arccos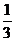
11.Ⅰ:总金额 y = a.( 1+ x% ). b ( 1- x%)
x%)
y =  ab (1+x%
) ( 2-x% )≤
ab (1+x%
) ( 2-x% )≤ ab.(
ab.(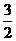 )2
1+x% = 2-x% 时“=”成立
)2
1+x% = 2-x% 时“=”成立
x% =  =
50% 价格上涨50%
=
50% 价格上涨50%
Ⅱ:y = ab( 1+ x% ) ( 1-kx%) y = ab[-k (x% )2+( 1-k) x%+1 ]
∴y′
= ab.[(-2k)x% .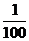 +(
1-k)
+(
1-k) 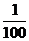 ] > 0 恒成立时
] > 0 恒成立时
说明y是不断递增 ∴0<k<1
12.Ⅰ:设不动点(x0 , x0)(-x0 , -x0)
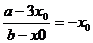
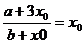 a = x02
b = 3
a = x02
b = 3
满足a > 0 且a≠9 b = 3
Ⅱ: a = 8
f ( x ) = 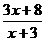
 :y = x
:y = x
p ( xp , 3-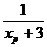 )
3-
)
3-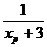 > 3 xp
<-3
> 3 xp
<-3
d = 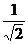 .
.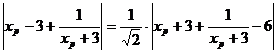 xp+3
< 0
xp+3
< 0
∴ d = 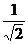 .(
.(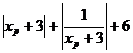 )≥
)≥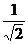 .(2+6)=
4
.(2+6)=
4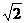
xp+3
= -1时 即xp = -4时
dmin = 4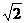 , P(-4 , 4)
, P(-4 , 4)