
网址:http://www.1010jiajiao.com/paper/timu/5153635.html[举报]
12.已知函数f ( x )的定义域为D,若存在x0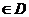 ,使f ( x0 ) = x0 ,则称点是函数f
( x )的不动点。(Ⅰ)若f ( x )=
,使f ( x0 ) = x0 ,则称点是函数f
( x )的不动点。(Ⅰ)若f ( x )=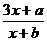 有两个关于原点对称的不动点,求实数a、b应满足的条件;(Ⅱ)在(Ⅰ)的条件下,若a = 8,记f ( x )的两个不动点为A、B,P为f ( x )图象上的点,其纵坐标yp>3,求点P到直线AB的距离的最小值及点P。
有两个关于原点对称的不动点,求实数a、b应满足的条件;(Ⅱ)在(Ⅰ)的条件下,若a = 8,记f ( x )的两个不动点为A、B,P为f ( x )图象上的点,其纵坐标yp>3,求点P到直线AB的距离的最小值及点P。
[参考答案]
联想与激活(5)
1.C 联想:(1)A
(2)y = -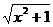 (x≥0) (3)9
(x≥0) (3)9
(4)t≤ (5)D
(6)C
(5)D
(6)C
2.C 联想:(1)①②③ (2)a
=  (3)A
(4)
(3)A
(4)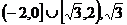
3.B 联想:(1)B (2)A (3)4 (4)12
4.A 联想:(1)C (2)x+y
= 3 (3)y2-x2
= 
(4)-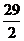 (5)
(5)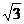 ,1200
(6)-34
,1200
(6)-34
5.B 联想:(1)B (2)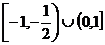 (3)
(3)
6.A 联想:(1)A (2)3 (3)A (4)D
7.D 联想:(1)A (2)B
(3)C (4)-3x4-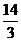 x3
(5)[ 1,
x3
(5)[ 1,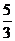 ]
]
8.B 联想:(1)B (2)10 (3)C
9.C 联想:(1)1 (2)8
10.C 联想: D
11. 2联想:(1)( x-1)2 = 4(y+1) (2)( y+6 )2 = 8(x+6)
12.解:(I)设F(C,O)(C>O)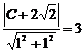 C=
C=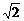 又b=1,
∴a=3
又b=1,
∴a=3
∴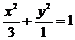
(II)假设这样的直线存在,交于两点(x1,y1)(x2,y2)
则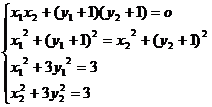
利用中点在椭圆的内部求出k的范围是(-1,0)∪(0,1)
联想与激活(6)
1.B
联想:(1)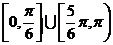 (2)B (3)C
(2)B (3)C
2.B 联想:(1)B (2)0<a<1时,x>1;a>1时,0<x<1
(3)a>1时,x∈(-1,0);0<a<1时,x∈(-2,-1)
3.A 联想:(1)D (2)A (3)C (4)m>7
4.B
联想:(1)D (2)cos4x或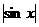 (3)f
(m-1)>0
(3)f
(m-1)>0
5.A
联想:(1)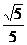 (2)
(2)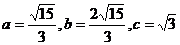 (3)
(3)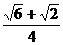
(4)①A=45°,B=60°,C=75°
②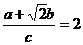
设A=60°-α,C=60°+α
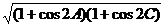 =2cosAcosC=cos(A+C)+cos(A-C)=cos120°+cos2α=
=2cosAcosC=cos(A+C)+cos(A-C)=cos120°+cos2α=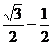
∴cos2α=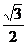 α=15°
∴A=45°,C=75°
α=15°
∴A=45°,C=75°
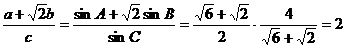
(5) ①cosa=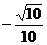 ②f-1(
②f-1(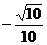 )=
)=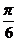
2a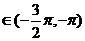 ∴cos2
∴cos2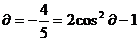
2cos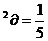 cos
cos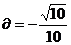
f(x)=-2cos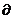 sinX+2cos
sinX+2cos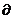 ∴-2cos
∴-2cos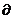 sinx+2cos
sinx+2cos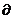 =-
=-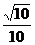
∴-2sinx+2=1
sinx= x=
x=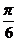 f-1(-
f-1(-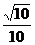 )=
)=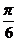
6. C 联想:(1)C (2)B (3)93
(4)an=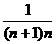 (5) ①{bn}为A.P
(5) ①{bn}为A.P
bn≠o,
2b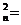 anan+1, an+1=bnbn+1,an=bn-1bn
anan+1, an+1=bnbn+1,an=bn-1bn
∴2b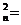 bn(bn-1+bn+1)
2bn = bn-1+bn+1
bn(bn-1+bn+1)
2bn = bn-1+bn+1
②2b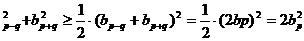
③3 a1+a2=2b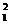 ∴a2=3
a2=b1b2 b2=
∴a2=3
a2=b1b2 b2=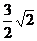
∴d=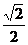 ∴bn=
∴bn=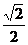 n ∴an=bn-1bn=
n ∴an=bn-1bn=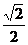 (n-1).
(n-1).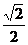 n=
n=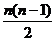 (n≥2)
(n≥2)
∴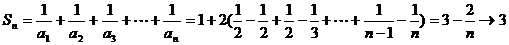
7.B
联想:(1)C (2)19
(3)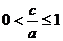 (4)5,5
(4)5,5
8.- 联想:I.圆
II.
联想:I.圆
II.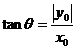
设p(x,y) 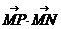 =2x+2
=2x+2
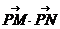 =x2-1+y2
=x2-1+y2
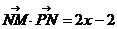 ∴2x=x2-1+y2
(x-1)2+y2=2
∴2x=x2-1+y2
(x-1)2+y2=2
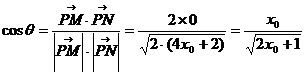
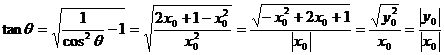 (x0≥0)
(x0≥0)
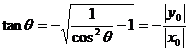 (x0<0
(x0<0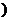 ∴
∴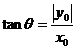
9.D
联想:(1)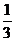 (2)D
(3)
(2)D
(3)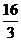 (4)
(4) ≤e<1
≤e<1
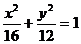
①B(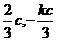 )
∴
)
∴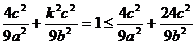 ∴4e4-37e2+9≤0
∴4e4-37e2+9≤0
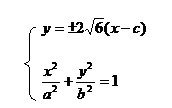
 ≤e≤3又e<1
∴
≤e≤3又e<1
∴ ≤e≤1
≤e≤1
②e=
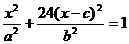
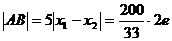 ∴
∴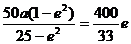 a=4
a=4
∴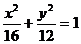
10.B
联想:(1)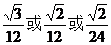 (答案不唯一) (2)A (3)B
(答案不唯一) (2)A (3)B
(4)I:证:正△ABC中,作BC边上高AF,交BC于F
交DE于G,则AG⊥DE,DE⊥FG。
∴A′G⊥DE,FG⊥DE A′G交FG于面A′GF ∴面DE⊥A′GF
DE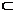 面BCED
∴面A′GF⊥面BCED
面BCED
∴面A′GF⊥面BCED
Ⅱ:过A′作A′M⊥AF于M,连EM。
面A′GF⊥面BCED A′M⊥AF 易知A′M⊥面ABC 又A′E⊥BD
∴EM⊥AB 则AM=2MG 如图
 A′G = AG =
3MG ∴cos∠A′GM
=
A′G = AG =
3MG ∴cos∠A′GM
= 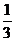
∠A′GM
= π-arccos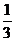
A′G⊥DE , FG⊥DE ∴∠A′GF为所求二面角的平面角
∴所求二面角为π-arccos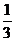
11.Ⅰ:总金额 y = a.( 1+ x% ). b ( 1- x%)
x%)
y =  ab (1+x%
) ( 2-x% )≤
ab (1+x%
) ( 2-x% )≤ ab.(
ab.(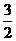 )2
1+x% = 2-x% 时“=”成立
)2
1+x% = 2-x% 时“=”成立
x% =  =
50% 价格上涨50%
=
50% 价格上涨50%
Ⅱ:y = ab( 1+ x% ) ( 1-kx%) y = ab[-k (x% )2+( 1-k) x%+1 ]
∴y′
= ab.[(-2k)x% .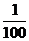 +(
1-k)
+(
1-k) 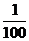 ] > 0 恒成立时
] > 0 恒成立时
说明y是不断递增 ∴0<k<1
12.Ⅰ:设不动点(x0 , x0)(-x0 , -x0)
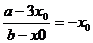
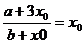 a = x02
b = 3
a = x02
b = 3
满足a > 0 且a≠9 b = 3
Ⅱ: a = 8
f ( x ) = 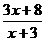
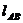 :y = x
:y = x
p ( xp , 3-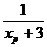 )
3-
)
3-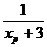 > 3 xp
<-3
> 3 xp
<-3
d = 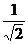 .
.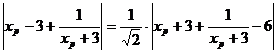 xp+3
< 0
xp+3
< 0
∴ d = 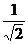 .(
.(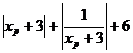 )≥
)≥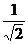 .(2+6)=
4
.(2+6)=
4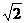
xp+3
= -1时 即xp = -4时
dmin = 4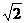 , P(-4 , 4)
, P(-4 , 4)