网址：http://www.1010jiajiao.com/paper/timu/5153689.html[举报]

5、抛物线的顶点在原点，焦点在x轴的正半轴上，直线x+y-1=0与抛物线相交于A、B两点，且|AB|=.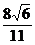

(1)求抛物线的方程；

(2)在x轴上是否存在一点C，使△ABC为正三角形？若存在，求出C点的坐标：若不存在，请说明理由。

解：(1)设所求抛物线方程为，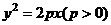

则由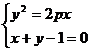消支y得　x²-2(1+p)x+1=0

设A(x₁，y₁)、B(x₂，y₂)

则x₁+ x₂＝2(1+p) 　　x₁x₂＝1

由弦长|AB|=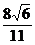建立关于p的方程.

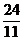解得　 p=或p=-(舍去)

故抛物线方程为.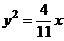　

(2)设AB的中点为D则D(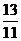，-)，x轴上存在满足条件的点C(x₀,0)，

由于△ABC为正三角形.所以CD⊥AB，|CD|=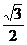|AB|=.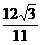

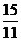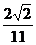
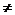
由CD⊥AB得x₀＝　　但|CD|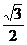＝|AB|=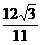

故x轴上不存在点C，使△ABC为正三角形。