
网址:http://www.1010jiajiao.com/paper/timu/5153878.html[举报]
17.(本小题满分12分)
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,记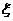 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求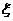 的分布列和期望.
的分布列和期望.
数学(理工农医类)参考答案
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.C 2.D 3.B 4.A 5.C 6.B 7.C 8.D 9.D 10.B
二、填空题:本大题共5小题,每小题5分,共25分.把答案填在横线上.
11.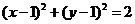
12.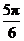
13.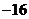
14.(1)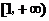 (2)
(2)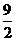
15.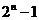 ,32
,32
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.解:(I)由题设知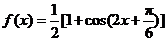 .
.
因为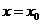 是函数
是函数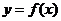 图象的一条对称轴,所以
图象的一条对称轴,所以
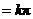 ,
,
即 (
(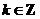 ).
).
所以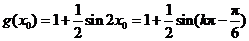 .
.
当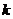 为偶数时,
为偶数时,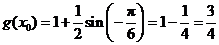 ,
,
当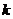 为奇数时,
为奇数时,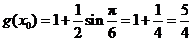 .
.
(II)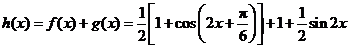
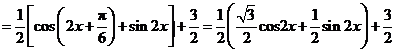
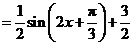 .
.
当 ,即
,即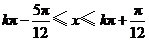 (
(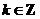 )时,
)时,
函数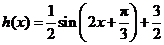 是增函数,
是增函数,
故函数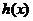 的单调递增区间是
的单调递增区间是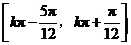 (
(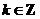 ).
).
17.解:任选1名下岗人员,记“该人参加过财会培训”为事件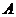 ,“该人参加过计算机培训”为事件
,“该人参加过计算机培训”为事件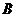 ,由题设知,事件
,由题设知,事件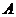 与
与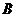 相互独立,且
相互独立,且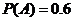 ,
,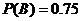 .
.
(I)解法一:任选1名下岗人员,该人没有参加过培训的概率是
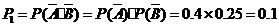
所以该人参加过培训的概率是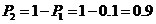 .
.
解法二:任选1名下岗人员,该人只参加过一项培训的概率是

该人参加过两项培训的概率是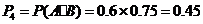 .
.
所以该人参加过培训的概率是 .
.
(II)因为每个人的选择是相互独立的,所以3人中参加过培训的人数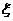 服从二项分布
服从二项分布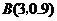 ,
,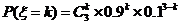 ,
,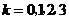 ,即
,即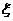 的分布列是
的分布列是
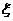 |
0 |
1 |
2 |
3 |
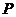 |
0.001 |
0.027 |
0.
243 |
0.729 |
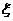 的期望是
的期望是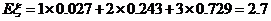 .
.
(或 的期望是
的期望是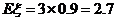 )
)
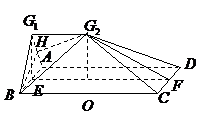 18.解:解法一:(I)因为平面
18.解:解法一:(I)因为平面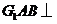 平面
平面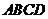 ,平面
,平面 平面
平面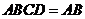 ,
,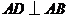 ,
,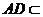 平面
平面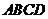 ,所以
,所以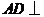 平面
平面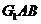 ,又
,又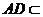 平面
平面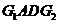 ,所以平面
,所以平面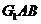
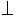 平面
平面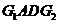 .
.
(II)过点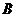 作
作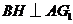 于点
于点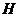 ,连结
,连结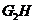 .
.
由(I)的结论可知,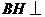 平面
平面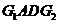 ,
,
所以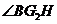 是
是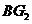 和平面
和平面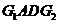 所成的角.
所成的角.
因为平面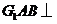 平面
平面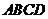 ,平面
,平面 平面
平面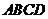
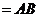 ,
,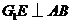 ,
,
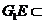 平面
平面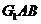 ,所以
,所以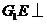 平面
平面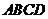 ,故
,故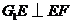 .
.
因为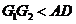 ,
,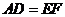 ,所以可在
,所以可在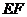 上取一点
上取一点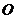 ,使
,使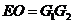 ,又因为
,又因为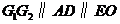 ,所以四边形
,所以四边形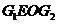 是矩形.
是矩形.
由题设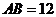 ,
,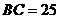 ,
,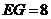 ,则
,则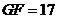 .所以
.所以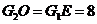 ,
,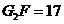 ,
,
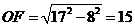 ,
,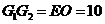 .
.
因为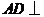 平面
平面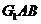 ,
, ,所以
,所以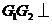 平面
平面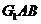 ,从而
,从而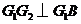 .
.
故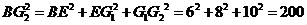 ,
,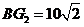 .
.
又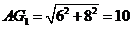 ,由
,由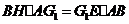 得
得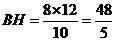 .
.
故 .
.
即直线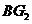 与平面
与平面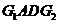 所成的角是
所成的角是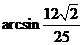 .
.
解法二:(I)因为平面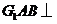 平面
平面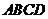 ,平面
,平面 平面
平面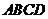
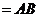 ,
,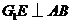 ,
,
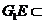 平面
平面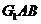 ,所以
,所以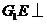 平面
平面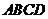 ,从而
,从而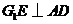 .又
.又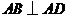 ,所以
,所以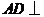 平面
平面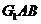 .因为
.因为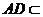 平面
平面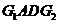 ,所以平面
,所以平面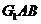
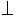 平面
平面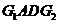 .
.
 (II)由(I)可知,
(II)由(I)可知,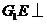 平面
平面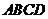 .故可以
.故可以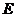 为原点,分别以直线
为原点,分别以直线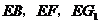 为
为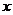 轴、
轴、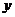 轴、
轴、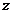 轴建立空间直角坐标系(如图),
轴建立空间直角坐标系(如图),
由题设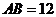 ,
,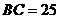 ,
,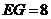 ,则
,则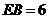 ,
,
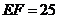 ,
,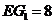 ,相关各点的坐标分别是
,相关各点的坐标分别是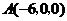 ,
,
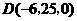 ,
,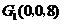 ,
, .
.
所以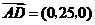 ,
,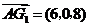 .
.
设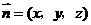 是平面
是平面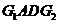 的一个法向量,
的一个法向量,
由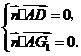 得
得 故可取
故可取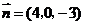 .
.
过点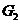 作
作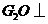 平面
平面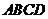 于点
于点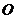 ,因为
,因为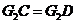 ,所以
,所以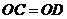 ,于是点
,于是点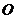 在
在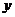 轴上.
轴上.
因为 ,所以
,所以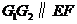 ,
,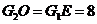 .
.
设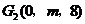 (
(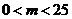 ),由
),由 ,解得
,解得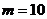 ,
,
所以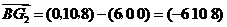 .
.
设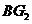 和平面
和平面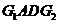 所成的角是
所成的角是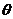 ,则
,则
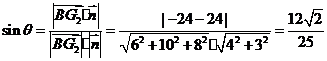 .
.
故直线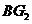 与平面
与平面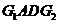 所成的角是
所成的角是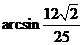 .
.
19.解:(I)如图,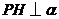 ,
,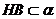 ,
,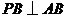 ,
,
由三垂线定理逆定理知,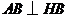 ,所以
,所以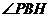 是
是
 山坡与
山坡与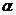 所成二面角的平面角,则
所成二面角的平面角,则 ,
,
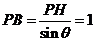 .
.
设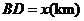 ,
, .则
.则
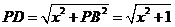
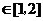 .
.
记总造价为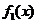 万元,
万元,
据题设有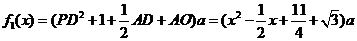

当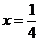 ,即
,即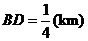 时,总造价
时,总造价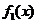 最小.
最小.
(II)设 ,
,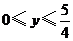 ,总造价为
,总造价为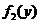 万元,根据题设有
万元,根据题设有
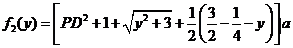
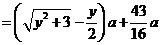 .
.
则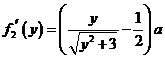 ,由
,由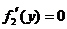 ,得
,得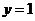 .
.
当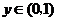 时,
时,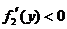 ,
,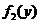 在
在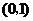 内是减函数;
内是减函数;
当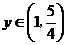 时,
时,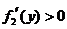 ,
,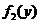 在
在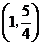 内是增函数.
内是增函数.
故当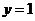 ,即
,即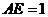 (km)时总造价
(km)时总造价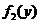 最小,且最小总造价为
最小,且最小总造价为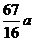 万元.
万元.
(III)解法一:不存在这样的点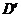 ,
,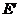 .
.
事实上,在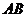 上任取不同的两点
上任取不同的两点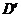 ,
,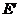 .为使总造价最小,
.为使总造价最小,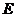 显然不能位于
显然不能位于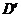 与
与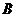 之间.故可设
之间.故可设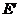 位于
位于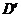 与
与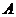 之间,且
之间,且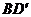 =
= ,
, ,
,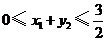 ,总造价为
,总造价为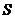 万元,则
万元,则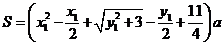 .类似于(I)、(II)讨论知,
.类似于(I)、(II)讨论知,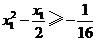 ,
,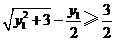 ,当且仅当
,当且仅当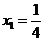 ,
,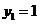 同时成立时,上述两个不等式等号同时成立,此时
同时成立时,上述两个不等式等号同时成立,此时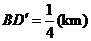 ,
,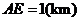 ,
,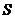 取得最小值
取得最小值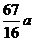 ,点
,点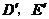 分别与点
分别与点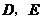 重合,所以不存在这样的点
重合,所以不存在这样的点
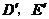 ,使沿折线
,使沿折线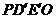 修建公路的总造价小于(II)中得到的最小总造价.
修建公路的总造价小于(II)中得到的最小总造价.
解法二:同解法一得
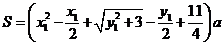
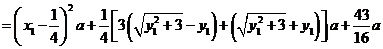
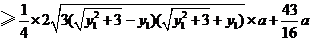
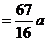 .
.
当且仅当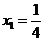 且
且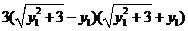 ,即
,即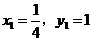 同时成立时,
同时成立时,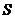 取得最小值
取得最小值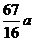 ,以上同解法一.
,以上同解法一.
20.解:由条件知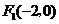 ,
,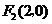 ,设
,设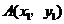 ,
,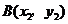 .
.
解法一:(I)设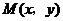 ,则
,则 则
则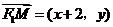 ,
,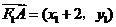 ,
,
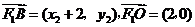 ,由
,由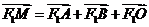 得
得
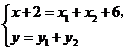 即
即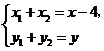
于是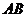 的中点坐标为
的中点坐标为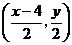 .
.
当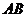 不与
不与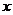 轴垂直时,
轴垂直时, ,即
,即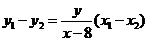 .
.
又因为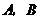 两点在双曲线上,所以
两点在双曲线上,所以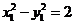 ,
,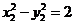 ,两式相减得
,两式相减得
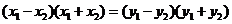 ,即
,即 .
.
将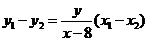 代入上式,化简得
代入上式,化简得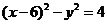 .
.
当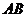 与
与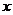 轴垂直时,
轴垂直时,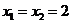 ,求得
,求得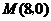 ,也满足上述方程.
,也满足上述方程.
所以点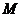 的轨迹方程是
的轨迹方程是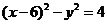 .
.
(II)假设在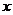 轴上存在定点
轴上存在定点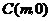 ,使
,使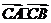 为常数.
为常数.
当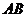 不与
不与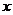 轴垂直时,设直线
轴垂直时,设直线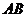 的方程是
的方程是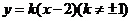 .
.
代入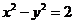 有
有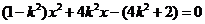 .
.
则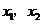 是上述方程的两个实根,所以
是上述方程的两个实根,所以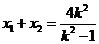 ,
, ,
,
于是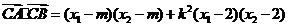

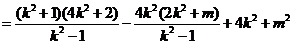
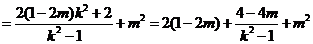 .
.
因为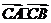 是与
是与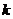 无关的常数,所以
无关的常数,所以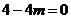 ,即
,即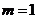 ,此时
,此时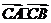 =
=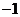 .
.
当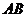 与
与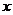 轴垂直时,点
轴垂直时,点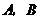 的坐标可分别设为
的坐标可分别设为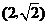 ,
,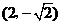 ,
,
此时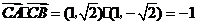 .
.
故在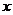 轴上存在定点
轴上存在定点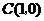 ,使
,使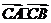 为常数.
为常数.
解法二:(I)同解法一的(I)有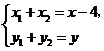
当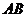 不与
不与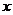 轴垂直时,设直线
轴垂直时,设直线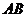 的方程是
的方程是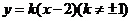 .
.
代入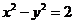 有
有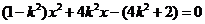 .
.
则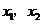 是上述方程的两个实根,所以
是上述方程的两个实根,所以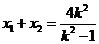 .
.
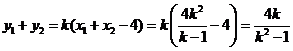 .
.
由①②③得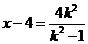 .…………………………………………………④
.…………………………………………………④
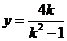 .……………………………………………………………………⑤
.……………………………………………………………………⑤
当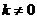 时,
时,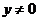 ,由④⑤得,
,由④⑤得,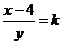 ,将其代入⑤有
,将其代入⑤有
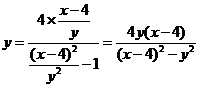 .整理得
.整理得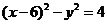 .
.
当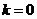 时,点
时,点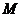 的坐标为
的坐标为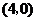 ,满足上述方程.
,满足上述方程.
当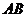 与
与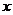 轴垂直时,
轴垂直时,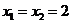 ,求得
,求得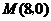 ,也满足上述方程.
,也满足上述方程.
故点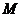 的轨迹方程是
的轨迹方程是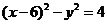 .
.
(II)假设在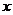 轴上存在定点点
轴上存在定点点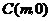 ,使
,使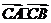 为常数,
为常数,
当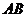 不与
不与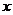 轴垂直时,由(I)有
轴垂直时,由(I)有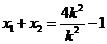 ,
, .
.
以上同解法一的(II).
21.解:(I)当 时,由已知得
时,由已知得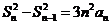 .
.
因为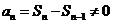 ,所以
,所以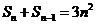 .
…… ①
.
…… ①
于是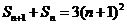 .
……②
.
……②
由②-①得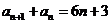 .
…… ③
.
…… ③
于是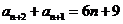 .
…… ④
.
…… ④
由④-③得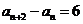 ,
…… ⑤
,
…… ⑤
所以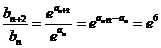 ,即数列
,即数列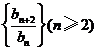 是常数数列.
是常数数列.
(II)由①有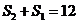 ,所以
,所以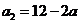 .由③有
.由③有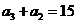 ,
,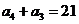 ,所以
,所以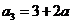 ,
,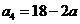 .
.
而 ⑤表明:数列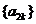 和
和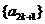 分别是以
分别是以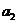 ,
,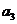 为首项,6为公差的等差数列,
为首项,6为公差的等差数列,
所以 ,
,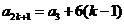 ,
,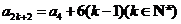 ,
,
数列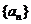 是单调递增数列
是单调递增数列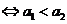 且
且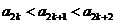 对任意的
对任意的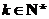 成立.
成立.
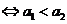 且
且
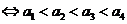
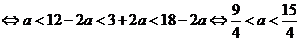 .
.
即所求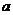 的取值集合是
的取值集合是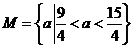 .
.
(III)解法一:弦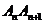 的斜率为
的斜率为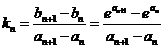
任取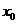 ,设函数
,设函数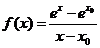 ,则
,则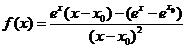
记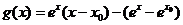 ,则
,则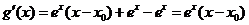 ,
,
当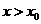 时,
时,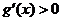 ,
,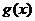 在
在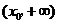 上为增函数,
上为增函数,
当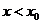 时,
时,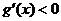 ,
,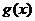 在
在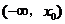 上为减函数,
上为减函数,
所以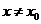 时,
时,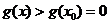 ,从而
,从而 ,所以
,所以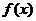 在
在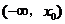 和
和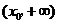 上都是增函数.
上都是增函数.
由(II)知,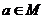 时,数列
时,数列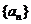 单调递增,
单调递增,
取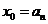 ,因为
,因为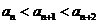 ,所以
,所以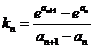
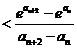 .
.
取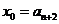 ,因为
,因为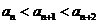 ,所以
,所以
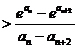 .
.
所以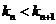 ,即弦
,即弦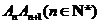 的斜率随
的斜率随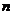 单调递增.
单调递增.
解法二:设函数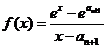 ,同解法一得,
,同解法一得,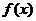 在
在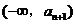 和
和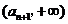 上都是增函数,
上都是增函数,
所以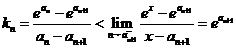 ,
, .
.
故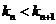 ,即弦
,即弦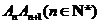 的斜率随
的斜率随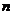 单调递增.
单调递增.