
网址:http://www.1010jiajiao.com/paper/timu/5154678.html[举报]
7.已知正三棱柱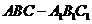 的侧棱长与底面边长相等,则
的侧棱长与底面边长相等,则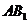 与侧面
与侧面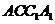 所成角的正弦值等于( )
所成角的正弦值等于( )
A.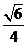 B.
B.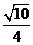 C.
C.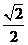 D.
D.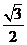
理科数学试题(必修+选修Ⅱ)参考答案
评分说明:
1. 本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分参考制订相应的评分细则.
2. 对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度.可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3. 解答右侧所注分数,表示考生正确做到这一步应得的累加分数.
4. 只给整数分数.选择题和填空题不给中间分.
一、选择题
1.D 2.C 3.C 4.D 5.A 6.C
7.A 8.A 9.C 10.B 11.B 12.B
二、填空题
13.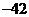 14.
14.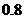 15.
15.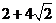 16.
16.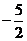
三、解答题
17.解:(1)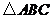 的内角和
的内角和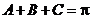 ,由
,由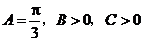 得
得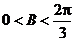 .
.
应用正弦定理,知
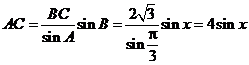 ,
,
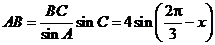 .
.
因为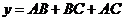 ,
,
所以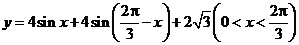 ,
,
(2)因为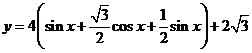
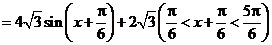 ,
,
所以,当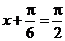 ,即
,即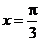 时,
时,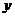 取得最大值
取得最大值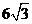 .
.
18.解:(1)记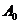 表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中无二等品”,
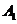 表示事件“取出的2件产品中恰有1件二等品”.
表示事件“取出的2件产品中恰有1件二等品”.
则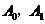 互斥,且
互斥,且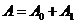 ,故
,故
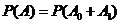
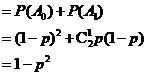
于是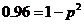 .
.
解得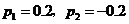 (舍去).
(舍去).
(2)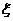 的可能取值为
的可能取值为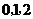 .
.
若该批产品共100件,由(1)知其二等品有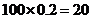 件,故
件,故
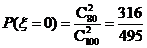 .
.
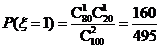 .
.
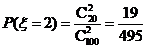 .
.
所以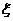 的分布列为
的分布列为
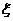 |
0 |
1 |
2 |
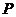 |
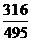 |
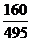 |
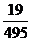 |
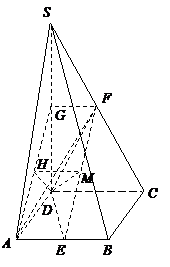 19.解法一:
19.解法一:
(1)作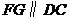 交
交 于点
于点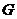 ,则
,则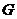 为
为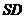 的中点.
的中点.
连结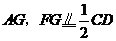 ,又
,又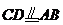 ,
,
故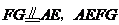 为平行四边形.
为平行四边形.
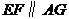 ,又
,又 平面
平面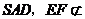 平面
平面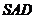 .
.
所以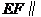 平面
平面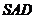 .
.
(2)不妨设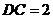 ,则
,则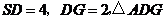 为等
为等
腰直角三角形.
取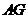 中点
中点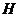 ,连结
,连结 ,则
,则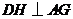 .
.
又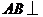 平面
平面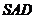 ,所以
,所以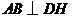 ,而
,而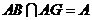 ,
,
所以 面
面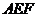 .
.
取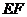 中点
中点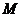 ,连结
,连结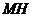 ,则
,则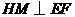 .
.
连结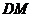 ,则
,则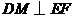 .
.
故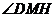 为二面角
为二面角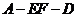 的平面角
的平面角

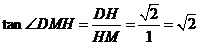 .
.
所以二面角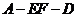 的大小为
的大小为 .
.
解法二:(1)如图,建立空间直角坐标系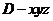 .
.
设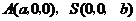 ,则
,则
 ,
,
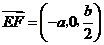 .
.
取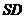 的中点
的中点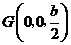 ,则
,则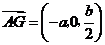 .
.
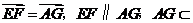 平面
平面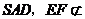 平面
平面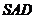 ,
,
所以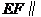 平面
平面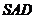 .
.
(2)不妨设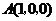 ,则
,则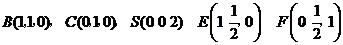 .
.
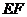 中点
中点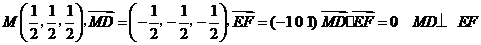
又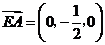 ,
,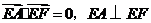 ,
,
所以向量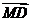 和
和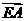 的夹角等于二面角
的夹角等于二面角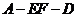 的平面角.
的平面角.
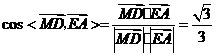 .
.
所以二面角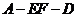 的大小为
的大小为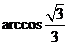 .
.
20.解:(1)依题设,圆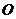 的半径
的半径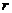 等于原点
等于原点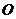 到直线
到直线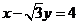 的距离,
的距离,
即 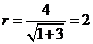 .
.
得圆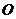 的方程为
的方程为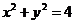 .
.
(2)不妨设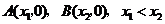 .由
.由 即得
即得
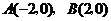 .
.
设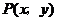 ,由
,由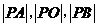 成等比数列,得
成等比数列,得
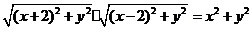 ,
,
即 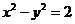 .
.

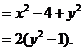
由于点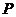 在圆
在圆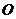 内,故
内,故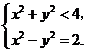
由此得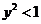 .
.
所以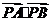 的取值范围为
的取值范围为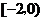 .
.
21.解:(1)由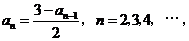
整理得  .
.
又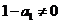 ,所以
,所以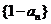 是首项为
是首项为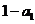 ,公比为
,公比为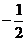 的等比数列,得
的等比数列,得
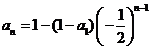
(2)方法一:
由(1)可知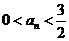 ,故
,故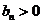 .
.
那么,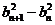
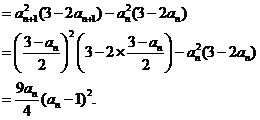
又由(1)知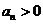 且
且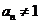 ,故
,故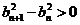 ,
,
因此 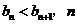 为正整数.
为正整数.
方法二:
由(1)可知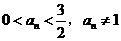 ,
,
因为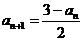 ,
,
所以 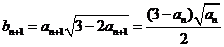 .
.
由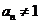 可得
可得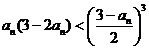 ,
,
即 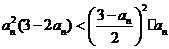
两边开平方得 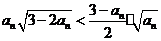 .
.
即 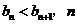 为正整数.
为正整数.
22.解:(1)求函数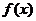 的导数;
的导数;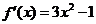 .
.
曲线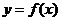 在点
在点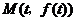 处的切线方程为:
处的切线方程为:
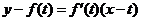 ,
,
即 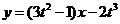 .
.
(2)如果有一条切线过点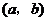 ,则存在
,则存在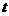 ,使
,使
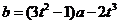 .
.
于是,若过点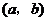 可作曲线
可作曲线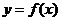 的三条切线,则方程
的三条切线,则方程
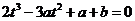
有三个相异的实数根.
记 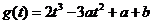 ,
,
则 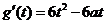
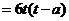 .
.
当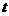 变化时,
变化时, 变化情况如下表:
变化情况如下表:
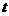 |
 |
0 |
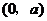 |
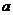 |
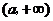 |
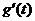 |
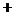 |
0 |
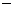 |
0 |
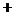 |
 |
 |
极大值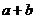 |
 |
极小值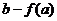 |
 |
由 的单调性,当极大值
的单调性,当极大值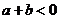 或极小值
或极小值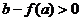 时,方程
时,方程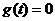 最多有一个实数根;
最多有一个实数根;
当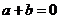 时,解方程
时,解方程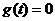 得
得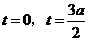 ,即方程
,即方程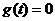 只有两个相异的实数根;
只有两个相异的实数根;
当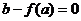 时,解方程
时,解方程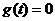 得
得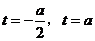 ,即方程
,即方程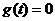 只有两个相异的实数根.
只有两个相异的实数根.
综上,如果过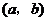 可作曲线
可作曲线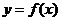 三条切线,即
三条切线,即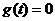 有三个相异的实数根,则
有三个相异的实数根,则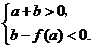
即 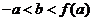 .
.